Задача 38936 помогите решить 2.1, 2.3 2.1. Чему...
Условие
2.1. Чему равно значение выражения ...
2.3. Найдите первообразную функции f(x) = 4x^3 - 4x + 6, график которой проходит через точку A (1; 5).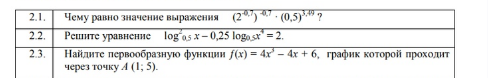
математика 10-11 класс
679
Все решения
2.3 F(x)=x^4-2x^2+6x+c
5=1^4-2*1^2+6*1+c ⇒ c=0
F(x)=x^4-2x^2+6x