Задача 38767 ...
Условие
а) Докажите, что DB⊥(ABC); б) Найдите косинус угла между плоскостями (ADC) и (ABC).
предмет не задан
1438
Все решения
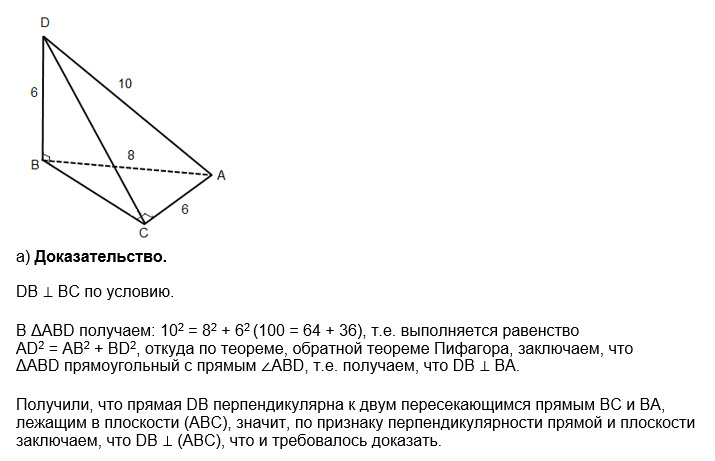

а) Докажите, что DB⊥(ABC); б) Найдите косинус угла между плоскостями (ADC) и (ABC).

