Задача 3866 Найдите точку минимума функции...
Условие
математика 10-11 класс
64946
Решение
2) Приравниваем ее к 0
3) Промежутки знакопостоянства и анализируем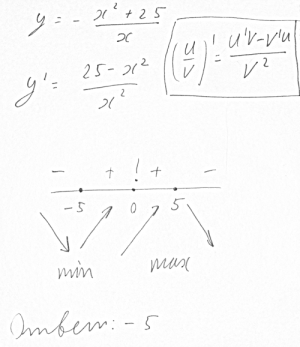
Ответ: -5
2) Приравниваем ее к 0
3) Промежутки знакопостоянства и анализируем
Ответ: -5