Задача 38590 ...

sova

2019-07-12 22:21:56

★

Пусть a и b - катеты прямоугольного треугольника,c - гипотенуза


Р(прямоугольного треугольника)=a+b+c

S=(1/2)a*b

По условию:
Р:S=2:3

2S=3P

Значит

[b]a*b=3*(a+b+c)[/b]

По теореме Пифагора:

[b]a^2+b^2=c^2[/b]

Система

{a^2+b^2=c^2
{ab = 3(a+b+c)

Произведение a*b кратно 3, значит либо а, либо b кратно 3

Рассмотрим числа, для которых справедлива теорема Пифагора.
( таких чисел бесчисленное множество)
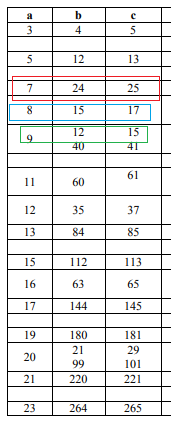
Cм. приложение.

Например, тройка чисел 7; 24 и 25 удовлетворяет указанным требованиям.
[b]Р=56[/b]
S=84

2S=3P -верно, так как 2*84=3*56

Тогда периметр

7+24+25=56

тройка чисел 8; 15 и 17 удовлетворяет указанным требованиям.
[b]Р=40[/b]
S=60

2S=3P -верно, так как 2*60=3*40

тройка чисел 9; 12 и 15 удовлетворяет указанным требованиям.
[b]Р=36[/b]
S=54

2S=3P -верно, так как 2*54=3*36