Задача 38588 ...

vk535418574

12 июля 2019 г. в 19:48

При каком значении а система неравенств имеет единственное решение:
{ 3/(x–a) ≥ 1
{ |x – 2a – 2| ≤ 1

sova

12 июля 2019 г. в 22:53

★

|x–2a–2| ≤ 1 ⇒ –1 ≤ x–2a–2 ≤ 1 ⇒ (x–3)/2≤ a ≤ (х–1)/2

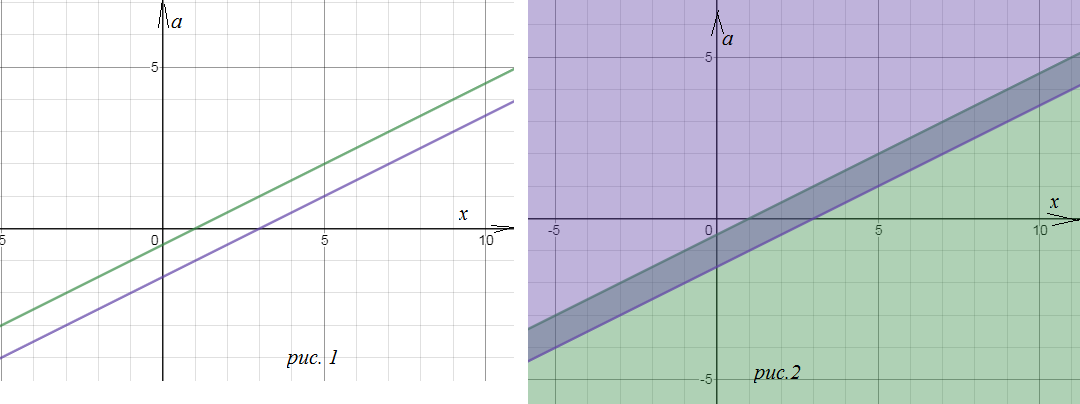
На пл. хОа cтроим графики a=(x–3)/2 и a=(x–1)/2

Получаем две прямые

см. рис.1

Неравенству

(x–3)/2≤ a ≤ (х–1)/2

удовлетворяют точки, расположенные между этими прямыми.

Cм. рис. 2

Неравенство:

3/(x–a) ≤ 1 или (3–x–a)/(x–a) ≤ 0

равносильно совокупности двух систем.
{3–x–a ≥ 0
{x–a <0

или

{3–x–a ≤ 0
{x–a >0

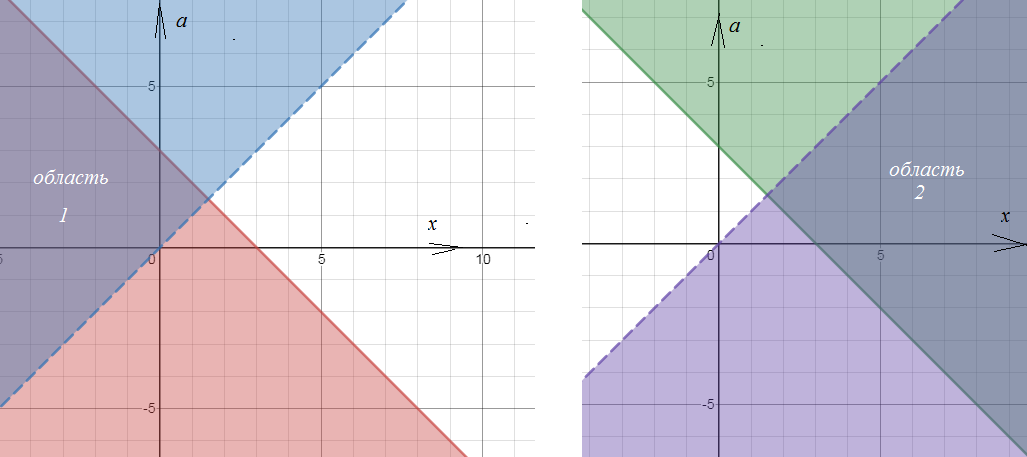
Строим прямые и заштриховываем соответствующие области:
см. рис. 3 и 4 ( область 1 соответствует первой системе, область 2 второй)

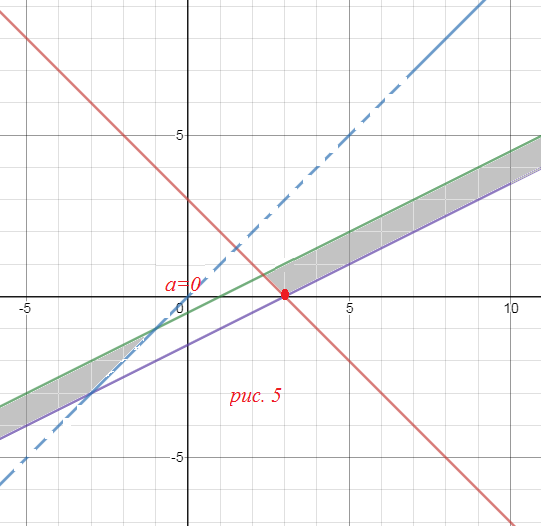
На рис. 5 закрашены области, удовлетворяющее системе.

При а=0 система имеет единственное решение х=3