Задача 38586 ...

sova

2019-07-12 22:07:04

★

cosπx = - x^2+6x-10

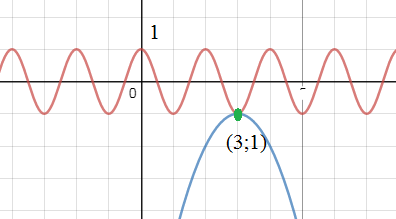
Решаем графически

y=cosπx

-1 ≤ сosπx ≤ 1

y=-x^2+6x-10 - парабола ветви вниз, наибольшее значение в точке

x_(o)=3

y_(o)=3^2-6*3+10= - 1


Значит, графики имеют единственное общее значение

при у= -1

cosπx= -1

πx=π+ 2πk, k ∈ Z

x=1+2k, k ∈ Z

x_(o)=3 получается из этой серии при k=1

О т в е т. (3;-1)