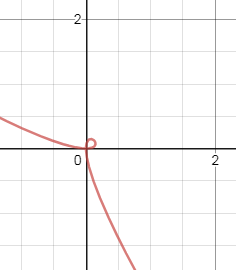
Задача 38471 3606. Область, ограниченной линией (x +...

foxy

1 июля 2019 г. в 16:32

3606. Область, ограниченной линией (x + y)³ = xy, лежащей в первом квадрате (четверть).

sova

1 июля 2019 г. в 17:24

★

Переходим к полярным координатам
x=rcos φ
y=rsin φ

(x+y)³=(rcos φ+rsin φ)³=r³(cos φ +sin φ )³

xy=rcos φ ·rsinφ =r²sinφcosφ


Уравнение петли:
r³(cos φ +sin φ )³=r²sinφcosφ

r=sinφcosφ/(sin φ+cos φ)³

0 ≤r ≤ sinφcosφ/(sin φ+cos φ)³
0 ≤ φ ≤ π/2


S= ∫ ∫ _Ddxdy= ∫^π/2₀dφ ∫ ^{sinφcosφ/(sin φ+cos φ)3}₀ rdr=

= ∫^π/2₀ (r²/2)|^{sinφcosφ/(sin φ+cos φ)3}₀ d φ=

=(1/2) ∫^π/2₀sin² φ cos² φdφ/(sin φ +cos φ )⁶

По формулам тригонометрии:

sin² φ cos² φ=(1/4)sin² 2φ

(sin φ +cos φ )⁶=((sin φ +cos φ )²)³=(sin²φ +2sinφcos φ+cos² φ)³= (1+sin2 φ)³

получаем

(1/8) ∫^π/2₀sin²2φ dφ/(1+sin2φ)³