Задача 38459 Помогите пожалуйста решить 2 уравнения! ...
Условие
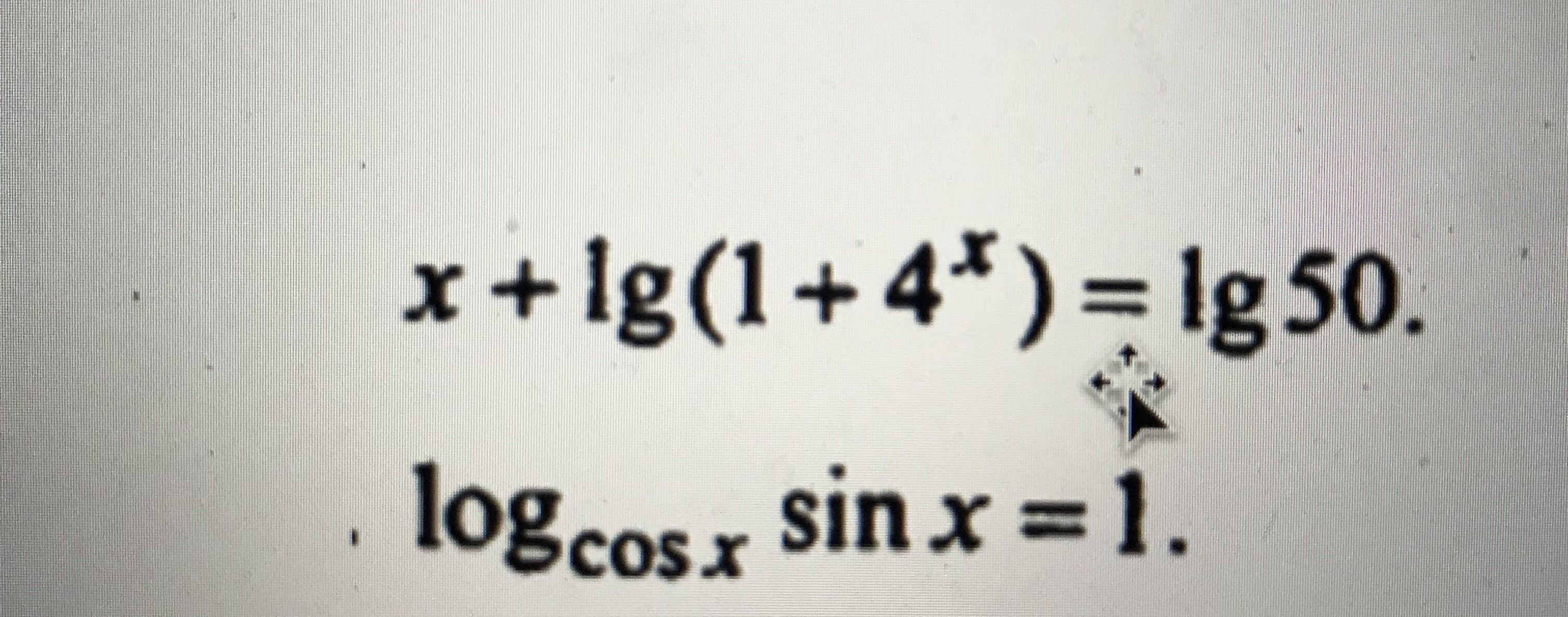
Все решения
x+lg(1+4^(x))=lg10^(x)+lg(1+4^(x))=lg(10^(x)*(1+4^(x))
Уравнение:
[b]lg(10^(x)*(1+4^(x))=lg50[/b]
lg(10^(x)*(1+4^(x))=lg50
10^(x)*(1+4^(x))=50
10^(x)+(10*4)^(x)=50
[b]10^(x)+(40)^(x)=50[/b]
Решаем графически
y=10^(x) возрастающая функция
y=(40)^(x) возрастающая функция
cумма возрастающих функций есть функция возрастающая.
y=50 - график прямая || оси Ох
Возрастающая функция слева и прямая || оси Ох пересекаются ровно в одной точке.
Это точка х=1
О т в е т. [b]х=1[/b]
2.
ОДЗ:
{sinx>0
{cosx>0
{cosx ≠ 1
log_(cosx)sinx=1 ⇒ (cosx)^(1)=sinx
sinx=cosx
Делим обе части уравнения на cosx ≠ 0
tgx=1
x=(π/4) +πk, k ∈ Z
ОДЗ удовлетворяют корни в первой четверти, при k=2n
О т в е т. (π/4) +2πn, n ∈ Z