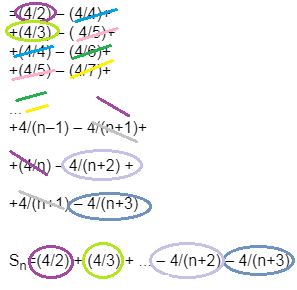Задача 38330 ...

vk436820776

23 июня 2019 г. в 13:35

Найти сумму ряда

1. ∑ (8 / (n² + 4n + 3)), n=1 до ∞

sova

23 июня 2019 г. в 14:09

★

Раскладываем дробь на простейшие.

n²+4n+3=(n+1)(n+3)

тогда

8/(n²+4n+3)= A/(n+1)+ B/(n+3)

8=(A+B)n+(3A+B)

A+B=0
3A+B=8

2A=8
A=4
B=–4

S_n= ∑ ⁿ₁(4/(k+1) – 4/(k+3))=

=(4/2) – (4/4)+
+(4/3) – ( 4/5)+
+(4/4) – (4/6)+
+(4/5) – (4/7)+

...
+4/(n–1) – 4/(n+1)+

+(4/n) – 4/(n+2) +

+4/(n+1) – 4/(n+3)


S_n=(4/2) + (4/3) + ... – 4/(n+2) – 4/(n+3)

=(10/3)+ ... – 4/(n+2) – 4/(n+3)

По определению:

S=lim_{n → ∞} S_n=10/3