Задача 38308 Найдите наибольшее значение суммы ,...
Условие
Найдите наибольшее значение суммы , где решение системы x+ y , где (x;y) решение системы
{(х^2=2x+y и y^2=2y+x
Решение

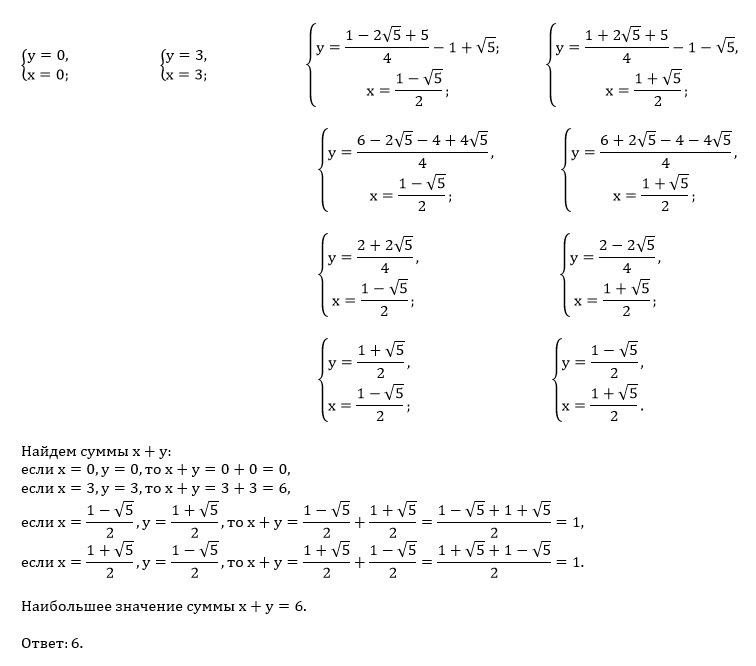
Все решения
{y^2=2y+x
(x^2-2x)^2=2*(x^2-2x)+x
x^4-4x^3+4x^2=2x^2-4x+x
x^4-4x^3+2x^2+3x=0
x*(x^3-4x^2+2x+3)=0
x*(x-3)*(x^2-x-1)=0
x_(1)=0 ⇒ y_(1)=0
или
x-3=0 ⇒ x_(2)=3;y_(2)=3
или
x^2-x-1=0
D=1+4=5
x_(3)=(1 - sqrt(5))/2 или x_(4)=(1 + sqrt(5))/2
y_(3)=(1 - sqrt(5))^2/4 - (1 - sqrt(5)) или y_(4)=(1 + sqrt(5))^2/4 - (1 + sqrt(5))
Выносим за скобки общий множитель:
y_(3)=(1 - sqrt(5))* [b]([/b](1 - sqrt(5))/4 - 1 [b])[/b] или y_(4)=(1 + sqrt(5))* [b]([/b](1 + sqrt(5))/4 - 1 [b])[/b]
y_(3)=(1 - sqrt(5))* [b]([/b](-3 - sqrt(5))/4 [b])[/b] или y_(4)=(1 + sqrt(5))* [b]([/b](-3 + sqrt(5))/4 [b])[/b]
y_(3)=(-3 +3 sqrt(5)-sqrt(5)+5)/4 или y_(4)=(-3 -3 sqrt(5)+sqrt(5)+5)/4
y_(3)=(1+ sqrt(5))/2 или y_(4)=(1 - sqrt(5))/2
Cистема имеет 4 решения:
(0;0)
(3:3);
((1-sqrt(5))/2;(1 + sqrt(5))/2)
((1+sqrt(5))/2;(1 - sqrt(5))/2)
x+y - наибольшая сумма 3+3=6
так как
(1-sqrt(5))/2 + (1 + sqrt(5))/2 = (1-sqrt(5)+1+sqrt(5))/2=1
О т в е т. 6