Задача 38277 system{x^2/y + y^2/x = 12;...
Условие
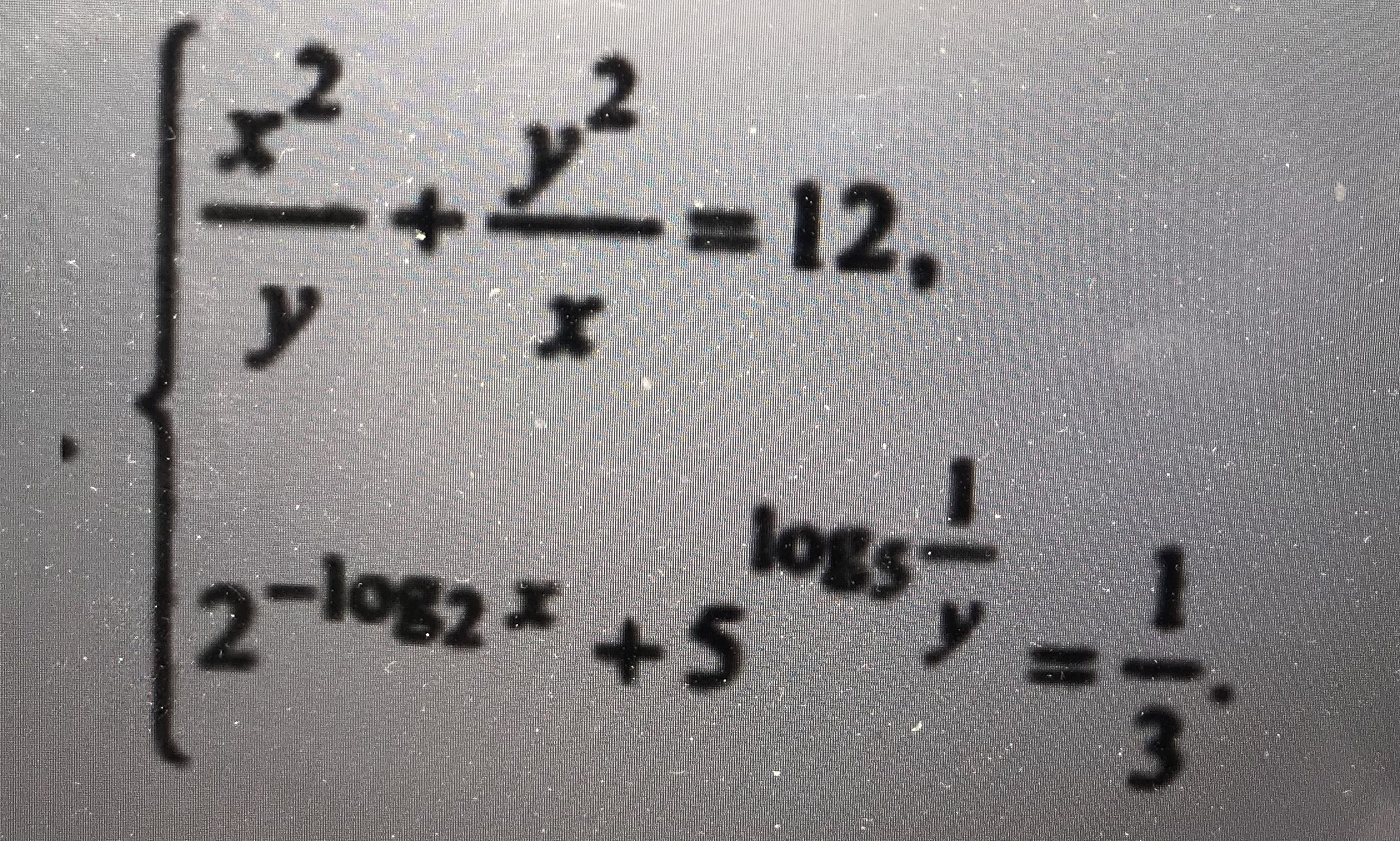
Все решения
x ≠0; y ≠0
умножаем на ху
[b]x^3+y^3=12xy[/b]
Второе:
Применяем основное логарифмическое тождество:
[b]a^(log_(a)b)=b[/b]
a>0; b>0; a ≠ 1
и свойство логарифма степени:
[b]log_(a)b^k=klog_(a)b[/b]
a>0; b>0; a ≠ 1
2^(-log_(2)x)=2^(log_(2)x^(-1))=x^(-1)=1/x
5^(log_(5)(1/y))=1/y
Второе уравнение при x >0; y>0 принимает вид:
[b](1/x)+(1/y)=1/3[/b]
Система
[b]{x^3+y^3=12xy
{(1/x)+(1/y)=1/3⇒ 3*(y+x)=xy
{x>0
{y>0[/b]
Подставляем из второго в первое вместо ху
x^3+y^3=36(x+y)
Так как x^3+y^3=(x+y)^3-3x^2y-3xy^2=(x+y)^3-3xy(x+y), то
Уравнение принимает вид:
(x+y)^3-3xy(x+y)=36(х+y)
(x+y)* [b]([/b](x+y)^2-3xy-36 [b])[/b]=0
x>0; y>0; значит x+y≠ 0
(x+y)^2-3xy-36=0
xy=3(x+y)
(x+y)^2-9*(x+y)-36=0
квадратное уравнение относительно x+y
Замена переменной:
x+y=t
t>0
t^2-9t-36=0
D=81-4*(-36)=81+144=225
t_(1)=(9-15)/2<0
t_(2)=(9+15)/2=12
Итак,
x+y=12
xy=3*(x+y)
xy=36
Решаем систему способом подстановки:
{x+y=12
{xy=36
[b]x=y=6[/b]
О т в е т. (6;6)