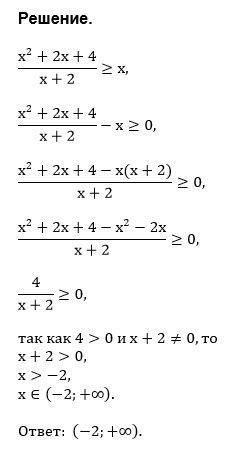Задача 38256 ...

natasha31275

2019-06-20 16:35:50

(x ^2+2x+4)/(x+2) ≥Х

sova

2019-06-20 17:01:27

Переносим х влево и сравниваем разность с нулем:

(x^2+2x+4)/(x+2)- x ≥ 0

Приводим к общему знаменателю:

(x^2+2x+4 - x *(x+2))/(x+2) ≥ 0

(x^2+2x+4 - x ^2-2x)/(x+2) ≥ 0

4/(x+2)≥ 0 ⇒ x+2≥ 0 и х+2≠0

Поэтому получаем

x+2 >0

х > -2

О т в е т. (-2;+ ∞ )