Задача 38250 ...
Условие


Решение
По определению:
F(x) первообразная функции на (a:b)
если для любого х∈(a,b)
F`(x)=f(x)
F`(x)=((x/2)-(3/x))`=(1/2)*x`-3*(1/x)`=(1/2)-3*(-1/x^2)=(1/2)+(3/x^2)=f(x)
2.
F(x)=-2*(-cosx)+C
F(x)=2cosx+C - общий вид первообразных
Подставляем координаты точки ( π/3;0)
0=2cos(π/3) + C
0=2*(1/2)+C
C=-1
F(x)=2cosx-1 - первообразная, проходящая через точку ( π/3;0)
3.
∫ e^(u)du=e^(u) + C
u=-2x
d(-2x)=-2dx ⇒ dx=d(-2x)/(2)
∫ e^(-2x)dx=∫ e^(-2x)d(-2x)/(-2)=(-1/2)∫ e^(-2x)d(-2x)= [b](-1/2) e^(-2x) + C[/b]
4.
а)
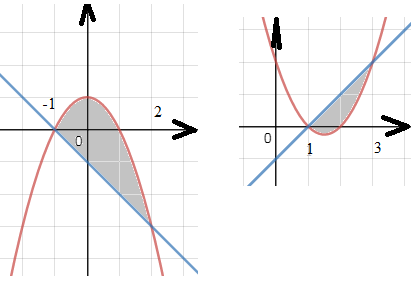
S= ∫ ^(2)_(-1) [b]([/b](1-x^2)-(-x-1) [b])[/b]dx =
= ∫ ^(2)_(-1) (1-x^2+x+1)dx= ∫ ^(2)_(-1) (2-x^2+x)dx=
= [b]([/b](2x- (x^3/3)+(x^2/2) [b])[/b]|^(2)_(-1)=
=
считаем самостоятельно
б)S= ∫ ^(3)_(1) [b]([/b](x^2-3х+2)-(x-1) [b])[/b]dx =
= ∫ ^(3)_(1)(x^2-3x+2-x+1)dx=
= ∫ ^(3)_(1)(x^2-4x+3)dx=
= [b]([/b](x^3/3)-4*(x^2/2)+3x [b])[/b]|^(3)_(1)=
cчитаем самостоятельно