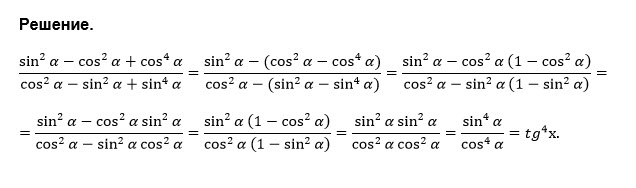Задача 38239 (Sin^2a-cos^2a+cos^4a)/(cos^2a-sin^2a+sin^4a)...

vk255777461

2019-06-19 17:52:12

(Sin^2a-cos^2a+cos^4a)/(cos^2a-sin^2a+sin^4a)

vk397114329

2019-06-19 23:00:04

( sin^2(a)-cos^2(a)+cos^4(a)/(cos^2(a)-sin^2(a)+sin^4(a))=
=(cos^4(a)-cos2a)/(sin^4(a)+cos2a)=(cos^4(a)-2cos^2(a)+1)/(sin^4(a)-2sin^2(a)+1)=((1-cos^2(a))^2/((1-sin^2(a))^2=(sin^2(a))^2/(cos^2(a))^2=tq^4(a).
Ответ: tq^4(a).