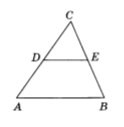
Задача 3823 В треугольнике ABC DE - средняя линия....
Условие
математика 8-9 класс
12069
Решение
S∆ABC = 4 ∙ S∆CDE = 4 ∙ 20 = 80.
Ответ: 80

S∆ABC = 4 ∙ S∆CDE = 4 ∙ 20 = 80.
Ответ: 80