Задача 38218 g(x)=4x/3-x...

vk443343151

2019-06-18 12:00:46

g(x)=4x/3-x

sova

2019-06-18 12:26:04

Это функция, обратная пропорциональность. График гипербола.

Область определения (- ∞;3)U(3;+ ∞ )

Производная

y`=((4x)`*(3-x)-4x*(3-x)`)/(3-x)^2

y`=(4*(3-x)-4x*(-1))/(3-x)^2

y`=(12-4x+4x)/(3-x)^2

y`=12/(3-x)^2

y` > 0 на (- ∞;3) и на (3;+ ∞ )

Функция возрастает на (- ∞;3) и на (3;+ ∞ )

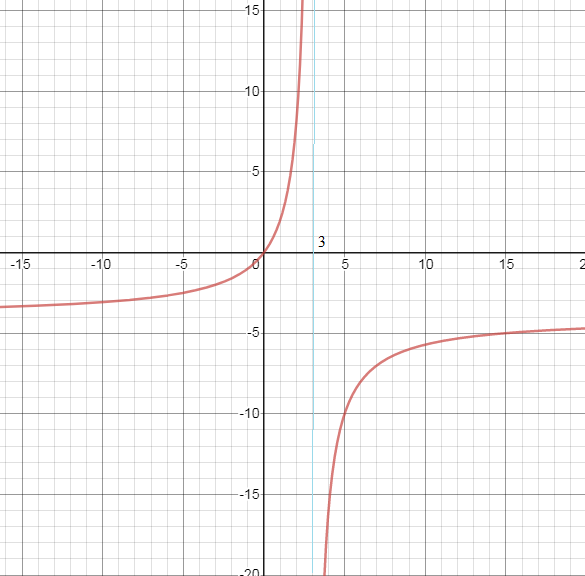
График см. рис.