Задача 38172 Постройте график функции y=x^4-4x^3+20 с...

kruzed1337

2019-06-15 18:14:36

Постройте график функции y=x^4-4x^3+20 с применением производной

sova

2019-06-15 22:30:02

Область определения (- ∞;+ ∞)

f`(x)=(x^4-4x^3+20)`=4x^3-12x^2

f`(x)=0

4x^3-12x^2=0

4х^2*(x-3)=0

x=0 или х= 3

Знак производной
__-_ (0) _-__ (3) __+__

y`< 0 на (- ∞; 0) и на (0;3)
значит функция убывает на (- ∞; 0) и на (0;3)

y`>0 на (3;+ ∞)
значит функция возрастает на (3;+ ∞)

x=3 - точка минимума, производная меняет знак с - на +

y``=12x^2-24x

y``=0

12x^2-24x=0

12x*(x-2)=0

x=0 и x=2

Знак второй производной

_+__ (0) _-_ (2) _+__

y``<0 на (0;2)
кривая выпукла вверх

y``<0 на (-∞;0) и на (2;+ ∞)
кривая выпукла вниз

x=0 и x=2 - точки перегиба

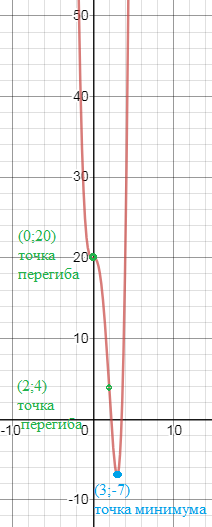
см. рис.