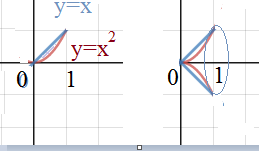Задача 38147 Найдите объем фигуры, полученного при...

vk503151203

2019-06-14 09:22:46

Найдите объем фигуры, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями графиком функции у=х^2, у=х.

sova

2019-06-14 09:28:05

V=π ∫ ^(b)_(a) ( f^2(x)-g^2(x))dx

V=π ∫ ^(1)_(0) ( (x)^2-(x^2)^2)dx= π ∫ ^(1)_(0) ( x^2-x^4)dx=

= [b]([/b](x^3/3)-(x^5/5) [b])[/b]|^(1)_(0)=(1/3)-(1/5)= [b]2/15[/b]