Задача 38133 Найти частное решение линейного...
Условие
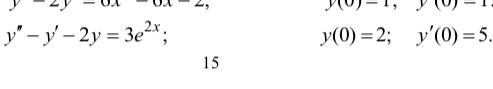
Решение
y``–y`-2y=0
Составляем характеристическое уравнение:
k^2–k-2=0
D=1+8=9
k_(1)=-1; k_(2)=2
y=C_(1)*e^(-x)+C_(2)*e^(2x) – общее решение однородного.
f(x)=3e^(2x)
y_(частное неоднородного)=A*x*e^(2x)
2 – корень характеристического уравнения кратности 1, поэтому умножаем на х ^(1)
y`_(частное неодн)=A*(x)`*e^(2x)+A*x*(e^(2x))`=
=A*e^(2x)+A*x*e^(2x)*(2x)`=
=A*e^(2x)+2*A*x*e^(2x)
y``_(частное неоднород)=2Ae^(2x) + 2*(A*e^(2x)+2*A*x*e^(2x))=
=4Ae^(2x)+4Axe^(2x)
Подставляем в данное уравнение
4Ae^(2x)+4Axe^(2x) - A*e^(2x)-2*A*x*e^(2x) -2A*x*e^(2x)=3e^(2x)
3A=3
A=1
y_(частное неодн)=x*e^(2x)
О т в е т. y=y_(общее однород)+y_(частн неодн)
y= C_(1)*e^(-x)+C_(2)*e^(2x) +x*e^(2x)
y`=-C_(1)e^(-x)+2C_(2)e^(2x)+e^(2x)+2x*e^(2x)
Так как
y(0)=2
y`(0)=5,
2=C_(1)*e^(0)+C_(2)*e^(0) +0*e^(0) ⇒ [b] С_(1)+С_(2)=2[/b]
5=-C_(1)e^(0)+2C_(2)e^(0)+e^(0)+2*0*e^(0) ⇒ [b]- С_(1)+2*С_(2)+1=5[/b]
3С_(2)=6
С_(2)=2
С_(1)=0
Решение удовлетворяющее начальным условиям ( решение задачи Коши)
y= 2*e^(2x) +x*e^(2x)