Задача 38104 Избавиться от алгебраической...
Условие
(a^2 - 3a +1)/(a^2 + 2a +1) где a корень уравнения x^3 + x^2 + 3x +4 = 0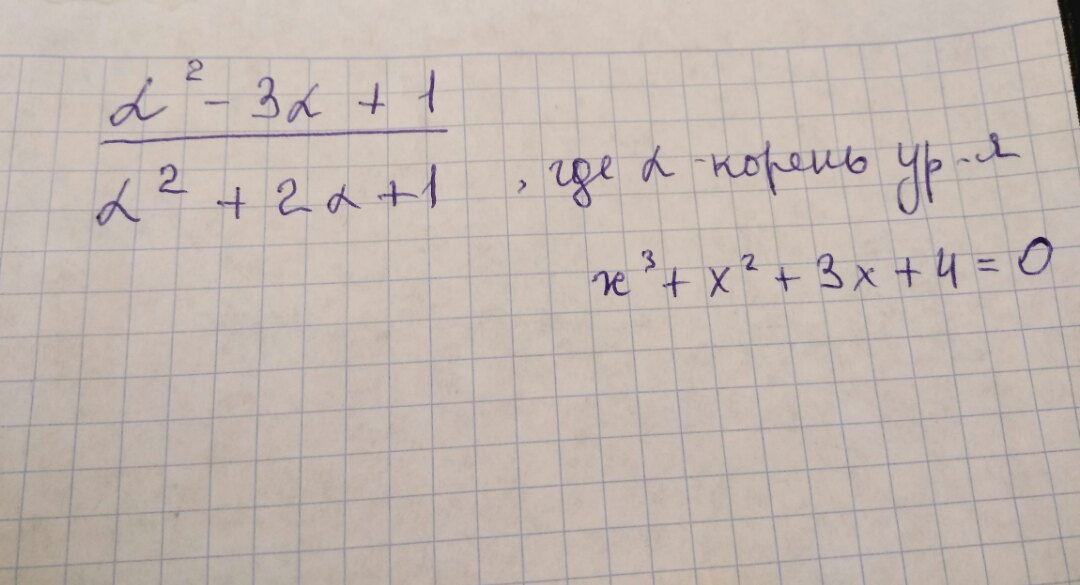
Решение
g(x)=x^3+x^2+3x+4
Делим
g(x) на f(x) "углом"
x^3+x^2+3x+4=(x^2+2x+1)*(x-1) + (4x+5)
Делим
x^2+2x+1 на (4х+5) "углом"
x^2+2x+1=(x+(5/4)*(x+(3/4) + (1/16)
Умножаем на 16
16x^2+32x+16=(4x+5)(4x+3) [b]+ 1[/b]
Последний ненулевой остаток равен 1
Значит можно представить так:
1=16*f(x)-(4x+5)(4x+3)
Но из равенства (x^3+x^2+3x+4=(x^2+2x+1)*(x-1) + (4x+5) или f(x)=g(x)*(x-1)+4x+5)
легко выразить
[b]4х+5=g(x)-f(x)*(x-1)[/b], тогда
1=16*f(x)-(4x+3)*g(x)+(4x+3)*(x-1)*f(x)
1=-(4x+3)* [b]g(x[/b])+(4x^2-x+13) [b]*f(x)[/b]
Так как
g(a)=0, то
1=(4a^2-a+13)*(a^2+2a+1)
1/(a^2+2a+1)=4a^2-a+13
Значит
[b](a^2-3a+1)/(a^2+2a+1)=(4a^2-a+13)*(a^2-3a+1)[/b]