Задача 38103 ...
Условие
15. log(1/5)(16-8x) ≤ log(1/5)(x^2-6x+8)-log(1/5)(x+5)
Решение
{16-8x>0 ⇒ x < 2
{x^2-6x+8 >0 ⇒ D=36-32=4; корни 2 и 4; ⇒ x < 2 или x >4
{x+5>0 ⇒ x > -5
ОДЗ: х ∈ (-5;2)
Запишем так:
log_(1/5)(16-8x) +log_(1/5)(x+5) ≤ log_(1/5)(x^2-6x+8)
Cумму логарифмов заменим логарифмом произведения
log_(1/5) (16-8x)(x+5) ≤ log_(0,1) (x^2-6x+8)
Логарифмическая функция с снованием (0 < 1/5 < 1) убывающая. Большему значению функции соответствует меньшее значение аргумента.
(16-8x)(x+5) ≤ (x^2-6x+8)
(x-2)(x-4) +8(x-2)(x+5) ≥ 0
(x-2)*(x-4+8x+40) ≥ 0
9*(х-2)*(х+4) ≥ 0
x ∈(- ∞ ;-4] U [2;+ ∞ )
С учетом ОДЗ получаем ответ:
(-5;-4]
13.
cos^2x=1-2sin^2x
Уравнение принимает вид:
1-2sin^2x+5sqrt(3)*sinx+8=0
-2sin^2x+5sqrt(3)*sinx+9=0
Квадратное уравнение относительно sinx
Замена переменной
sinx=t
2t^2-5sqrt(3)t-9=0
D=(-5sqrt(3))^2-4*2*(-9)=75+72=147
sqrt(147)=7sqrt(3)
t_(1)=(5sqrt(3)-7sqrt(3))/4; t_(2)=(5sqrt(3)+7sqrt(3))/4;
t_(1)=-sqrt(3)/2; t_(2)=3sqrt(3)
Обратно:
sinx=-sqrt(3)/2
х=(-1)^(k) arcsin(-sqrt(3))/2+πk, k ∈ Z
х=(-1)^(k)*(-π/3)+πk, k ∈ Z - о т в е т.
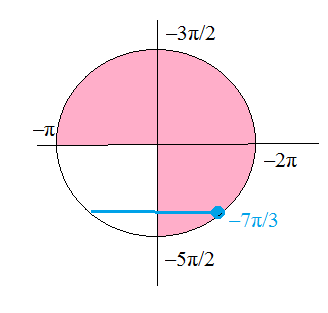
Отрезку [-5π/2;-π] принадлежит один корень
x=(-π/3)-2π=-7π/3
cм. рис.