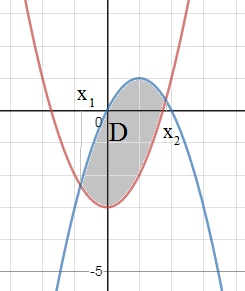Задача 38054 ...
Условие
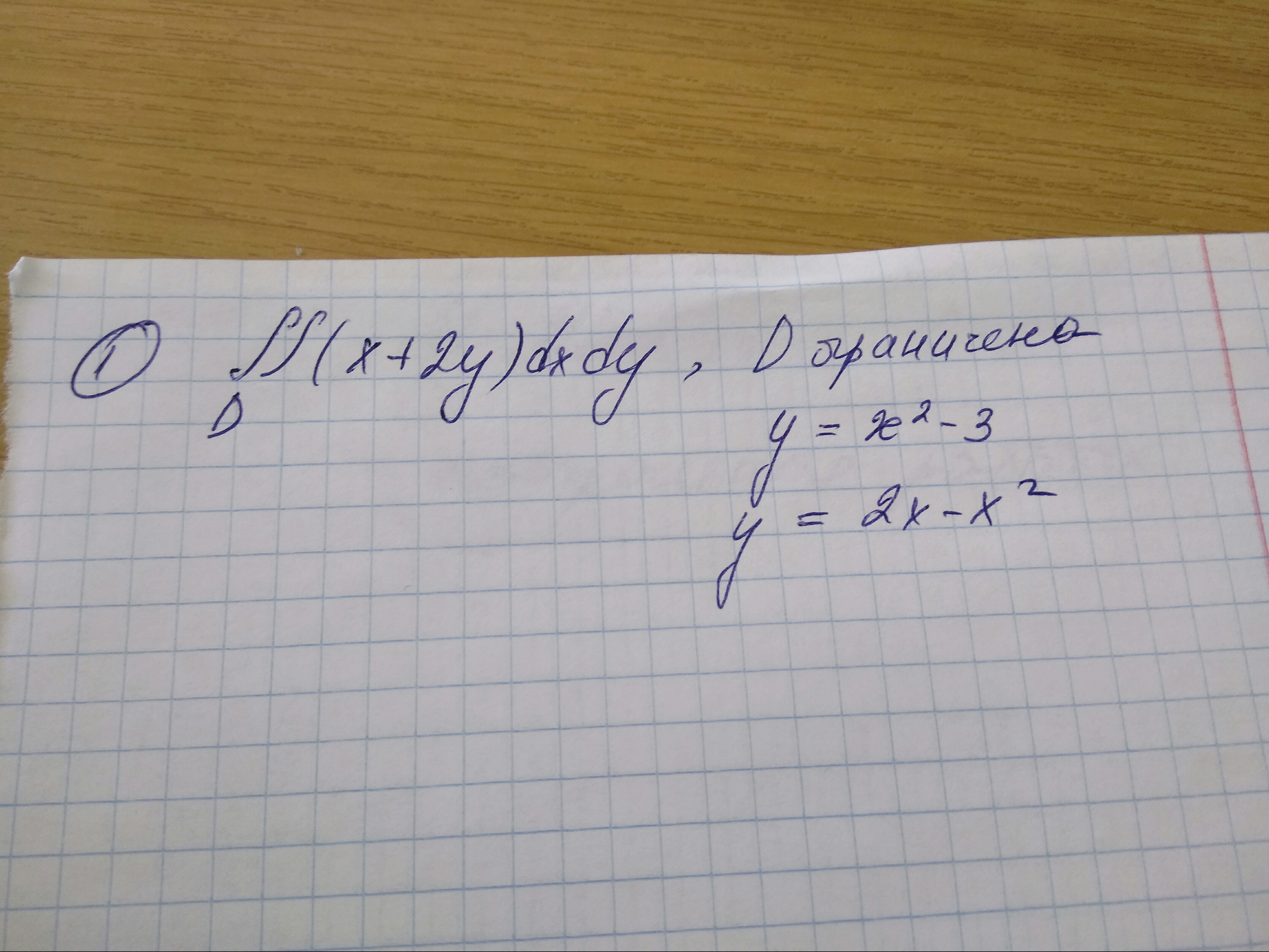
математика 10-11 класс
1197
Решение
★
y=x^2-3 и y=2x-x^2
x^2-3=2x-x^2
2x^2-2x-3=0
D=4-4*2*(-3)=28
x_(1)=(2-2sqrt(7))/4=(1-sqrtz(7))/2; х_(2)=(1+sqrt(7))/2
∫ ∫ _(D)(x+2y)dxdy= ∫ ^(x_(2))_(x_(1))dx ∫^(2x-x^2)_(x^2-3) (x+2y)dy=
= ∫ ^(x_(2))_(x_(1)) (xy+y^2)|^(y=2x-x^2)_(y=x^2-3)dx=
= ∫ ^(x_(2))_(x_(1))(x*(2x-x^2)-x*(x^2-3) +(2x-x^2)^2/2 - (x^2-3)^2/2)dx=
= ∫ ^(x_(2))_(x_(1)) (2x^2-x^3-x^3+3x+2x-2x^3+(x^4/2) - (x^4/2)+3x^2-(9/2))dx=
= ∫ ^(x_(2))_(x_(1)) (5x^2-4x^3+5x-(9/2))dx=
=(5(x^3/3)-4(x^4/4)+(5x^2/2)-(9/2)x)|^(x_(2))_(x_(1))=
где x_(1)=(1-sqrt(7))/2
x_(2)=(1+sqrt(7))/2