Задача 37925 Решите 4^x*2^(x^2+1) > 16 Вычислите...
Условие
Вычислите 5^(4log5sqrt(3)+1/2 log54)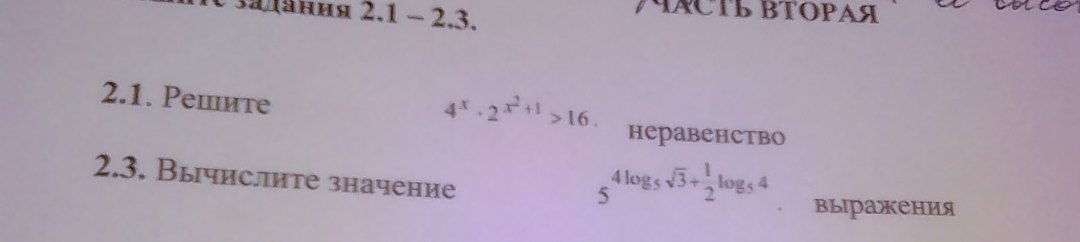
Решение
4=2^2
4^(x)=(2^2)^(x)=2^(2x)
4^(x)*2^(x^2+1)=2^(2x)*2^(x^2+1)=2^(x^2+2x+1)
16=2^4
Неравенство принимает вид:
2^(x^2+2x+1) > 2^(4)
Показательная функция с основанием 2 > 1 возрастающая, значит большему значению функции соответствует большее значение аргумента
x^2+2x+1 >4;
(x+1)^2-2^2 >0
Раскладываем а множители по формуле a^2-b^2=(a-b)(a+b)
(х+1-2)*(х+1+2) >0
(x-1)(x+3) > 0
Решаем методом интервалов.
Нули функции:
x-1=0 или х+3=0
х=1 или x=-3
___+__ (-3) ______ (1) ___+__
x ∈ (- ∞ ;-3) U (1;+ ∞ )
3.
a^(m+n)=a^(m)*a^(n)
5^(4log_(5)sqrt(3) + (1/2)log_(5)4)= 5^(4log_(5)sqrt(3)) * 5^((1/2)log_(5)4)
По свойству логарифма степени
log_(a)b^(k)=k*log_(a)b; a>0; a ≠1; b>0
и значит
k*log_(a)b=log_(a)b^(k)
Поэтому
5^(4log_(5)sqrt(3)) * 5^((1/2)log_(5)4)= 5^(log_(5)sqrt(3)^4) * 5^(log_(5)4^(1/2))
Основное логарифмическое тождество a^(log_(a)b)=b, a>0; a ≠1; b>0
Поэтому
5^(log_(5)sqrt(3)^4) * 5^(log_(5)4^(1/2))=sqrt(3)^4*4^(1/2)=9*2= [b]18[/b]
Все решение занимает две строчки:
5^(4log_(5)sqrt(3) + (1/2)log_(5)4)= 5^(4log_(5)sqrt(3)) * 5^((1/2)log_(5)4)=
=5^(log_(5)sqrt(3)^4) * 5^(log_(5)4^(1/2))=sqrt(3)^4*4^(1/2)=9*2= [b]18[/b]
