Задача 37920 Найти интеграл ...
Условие
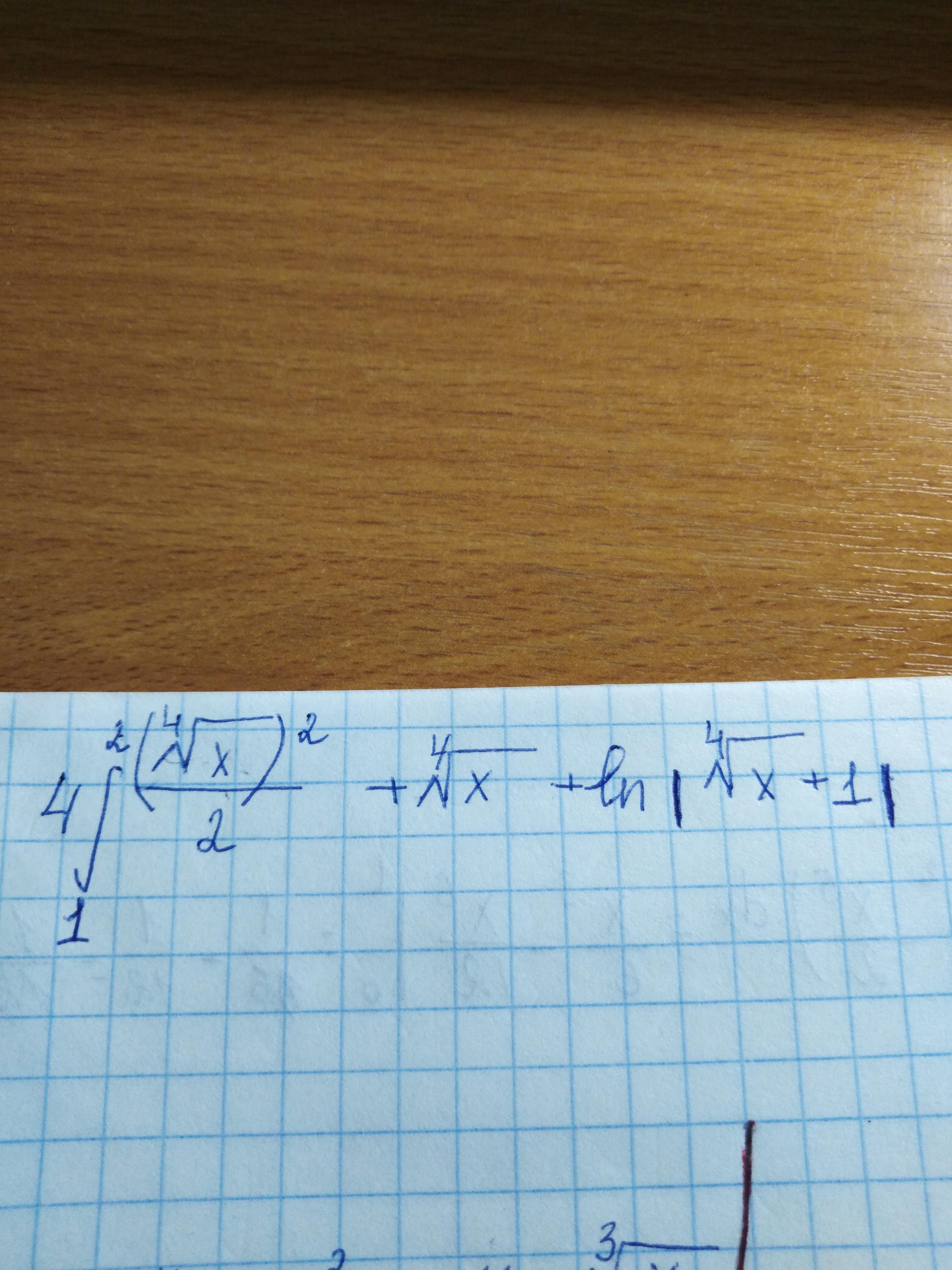
Все решения
Никакого модуля нет, есть круглые скобки.
Интеграл от суммы равен сумме интегралов.
Первый интеграл
∫ ^(2)_(1)sqrt(x)dx/2=(1/2) ∫ ^(2)_(1)x^(1/2)dx=(1/2)*x^(3/2)/(3/2)|^(2)_(1)=
=(1/3)*2^(3/2)-(1/3)*1^(3/2)= [b](2sqrt(2)-1)/3[/b]
Второй интеграл
∫ ^(2)_(1)x^(1/4)dx= x^(5/4)(5/4)|^(2)_(1)= (4/5)*(2^(5/4)-1^(5/4))=[b]
=(4/5)*(4sqrt(2)-1)[/b]
Третий интеграл
∫ ^(2)_(1) ln |x^(1/4)+1|dx= ∫ ^(2)_(1) ln (x^(1/4)+1)dx=
считаем по частям
Сначала замена переменной:
x^(1/4)=t
x=t^4
dx=4t^3dt
∫ ^(2)_(1) ln (x^(1/4)+1)dx= ∫ ^(16)_(1) ln (t+1)4t^3dt=
=4 ∫ ^(16)_(1)t^3ln(t+1)dx
u=ln(t+1)
du=dt/(t+1)
dv=t^3dt
v=(t^4/4)
=4*(t^4/4)*ln(t+1)|^(16)_(1)- 4∫^(16)_(1)(t^4/4)8(dt/(t+1)=
=t^4*ln(t+1) - ∫ ^(16)_(1)t^4dt/(t+1)=
Последний интеграл от дроби. Дробь неправильная. Надо выделить целую часть.
Сделаем это так:
t^4/(t+1)= (t^4-1+1)/(t+1)=(t^2-1)(t^2+1)/(t+1) + (1/(t+1))=
=(t-1)(t^2+1) + (1/(t+1))=
= [b]t^3-t^2+t-1 + (1/(t+1))[/b]
∫ ^(16)_(1)t^4dt/(t+1)= ∫ ^(16)_(1)(t^3-t^2+t-1 + (1/(t+1)))dt=
=((t^4/4) - (t^3/3)+(t^2/2) - t + ln |t+1|)|^(16)_(1)
Итак,
4* ∫^(2)_(1)(x^(1/4))^2/2 + x^(1/4) + ln | x^(1/4)+1|)dx=
=4* ∫ ^(2)_(1)sqrt(x)dx/2 + 4 * ∫ ^(2)_(1)x^(1/4)dx + 4 * ∫ ^(2)_(1) ln (x^(1/4)+1)dx=
=4*(1/2)*x^(3/2)/(3/2)|^(2)_(1)+ 4* (4/5)*(2^(5/4)-1^(5/4)) + 4 * (t^4*ln(t+1)|^(16)_(1) - ((t^4/4) - (t^3/3)+(t^2/2) - t + ln |t+1|)|^(16)_(1)=
= подставляем пределы и считаем самостоятельно
