Задача 37903 Решить уравнения...
Условие
cos(Pi+x)=sin(Pi/2)
cos^2x-sqrt(3)sinxcosx=0
Найти sina ...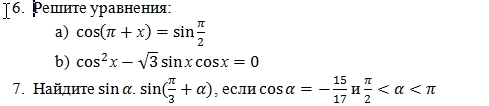
Решение
cos(π+x)=-cosx
sin(π/2)=1
Уравнение принимает вид:
-сosx=1
cosx=-1
x=π+2πn, n ∈ Z
О т в е т. π+2πn, n ∈ Z
б)
Разложим левую часть на множители:
cosx*(cosx-sqrt(3)sinx)=0
cosx=0 или сosx-sqrt(3)sinx=0
x=(π/2)+πk, k ∈ Z
сosx-sqrt(3)sinx=0
Однородное тригонометрическое уравнение.
Так как sinx и cosx одновременно не обращаются в 0, то делим либо на cosx ≠ 0, либо на sinx ≠ 0
tgx=1/sqrt(3)
x=(π/6)+πn, n∈ Z
О т в е т. (π/2)+πk, k ∈ Z; (π/6)+πn, n∈ Z
2.
sin( π/3)+ α)=sin (π/3)*cos α +cos(π/3)*sin α
sin^2 α =1-cos^2 α =1-(-15/17)^2=1-(225/289)=64/289
sin α =sqrt(64/289) =8/17
угол α во второй четверти, синус положителен
sin( π/3)+ α)=sin (π/3)*cos α +cos(π/3)*sin α =
=sqrt(3)/2)*(-15/17)+(1/2)*(8/17)=
= [b](-15sqrt(3)+8)/34[/b]
