Задача 37899 8. Докажите тождество:...

vk40624507

2019-06-03 17:51:54

8. Докажите тождество: sin^2a+ctg^2a+cos^2a = 1/sin^2a

9. Вычислите sin(-660)+cos 810

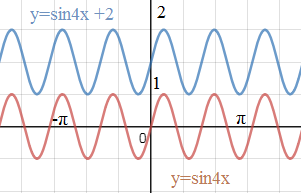
10. Постройте график y = sin4x+2

sova

2019-06-03 19:38:20

8.
sin^2 α +cos^2 α =1

sin^2 α +ctg^2 α +cos^2 α =(sin^2 α +cos^2 α )+ctg^2 α =

=1+(cos^2 α /sin^2 α )=(sin^2 α +cos^2 α )/sin^2 α=1/sin^2 α

9.
Период синуса и косинуса 360°
360° *n, n∈Z
так же являются периодами фнкций


sin(-660 ° )=sin(-720 °+60 °)=sin60 ° = sqrt(3)/2

cos810 ° =cos(720 ° +90 ° )=cos90 ° =0

О т в е т. ( sqrt(3)/2)+0= sqrt(3)/2

10
T=360 ° /4 - период функции y=sin4x

у=sin4x +2 получаем из графика y=sin4x
параллельным переносом на 2 единицы вверх вдоль оси Оу.