Задача 37887 ...

foxy

3 июня 2019 г. в 11:25

Решите неравенство

a) 3cos²x–4cosx ≥ 4

b) sinx+cosx > √2cos2x

sova

3 июня 2019 г. в 11:51

★

a) Замена переменной
cosx=t
3t²–4t–4 ≥ 0
D=(–4)²–4·3·(–4)=16+48=64
t₁=(4–8)/6=–4/6=–2/3; t₂=(4+8)/6=2

Решение неравенства
–2/3 ≤ t ≤ 2

Обратный переход от t к переменной х:

–(2/3) ≤ cosx ≤ 2

Двойное неравенство равносильно системе:
{cosx ≤ 2
{cosx ≥ (–2/3)

Первое неравенство верно при любом х, так как |cosx| ≤ 1

Решение неравенства
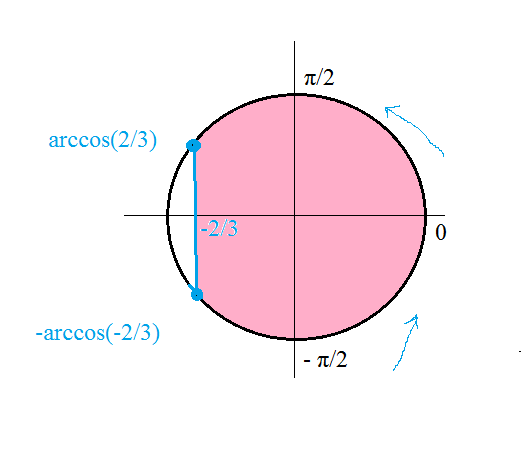
cosx ≥ –2/3
на единичной окружности

См. рис. 1
О т в е т. а) – arccos(–2/3)+2πn ≤ x ≤ arccos(–2/3)+2πn, n ∈Z
так как
arccos(–2/3)=π–arccos(2/3), то ответ можно записать в виде:

– (π–arccos(2/3))+2πn ≤ x ≤ π–arccos(2/3)+2πn, n ∈Z

или

–π+arccos(2/3))+2πn ≤ x ≤ π–arccos(2/3)+2πn, n ∈Z

б)
Делим обе части неравенства на √2

(1/√2)sinx + (1/√2)·cosx > cos2x
Так как
sin(π/4)=cos(π/4)=1/√2
неравенство примет вид:

sin(π/4)·sinx+cos(π/4)·cosx > cos2x

Применяем формулу

cos( α – β )=cos α ·cos β + sin α sinx β

cos(x–(π/4)) > cos2x

или

cos(x–(π/4)) – cos2x >0

или

cos2x–cos(x–(π/4)) < 0

Применяем формулу

cos α –cos β=–2sin((1/2)·(α – β))·sin((1/2)·(α + β))

–2·sin((2x–(x–(π/4))/2)·sin((2x+(x–(π/4))/2)<0

sin((x/2)+(π/8)) · sin((3x/2)–(π/8)) >0

Произведение положительно, когда множители имеют одинаковые знаки.
Получаем совокупность систем
(1)
{sin((x/2)+(π/8)) >0⇒ 2πm < (x/2)+(π/8) < π+2πm, m∈ Z
{sin((3x/2)–(π/8)) >0 ⇒ 2πn < (3x/2)–(π/8) < π+2πm, m ∈ Z

или

(2)
{sin((x/2)+(π/8)) <0 ⇒ – π+2πn < (x/2)+(π/8) < 2πn, n∈ Z
{sin((3x/2)–(π/8))<0 ⇒ –π+ 2πn < (3x/2)–(π/8) < 2πn, n ∈ Z



(1)
{–(π/8)+ 2πm < (x/2) < –(π/8)+ π+2πm, m∈ Z
{(π/8)+ 2πm < (3x/2) < π+(π/8)+2πm, m ∈ Z

или

(2)
{–(π/8) – π+2πn < (x/2) <–(π/8) +2πn, n∈ Z
{(π/8)–π+ 2πn < (3x/2) < (π/8 + 2πm, n ∈ Z


(1)
{–(π/4)+ 4πm < x < –(π/4)+2π+4πm, m∈ Z
{(π/12)+ (4π/3)·m < x) < (2π/3)+(π/12)+(4π/3)·m, m ∈ Z

или

(2)
{(π/4) – 2π+4πn < x <(π/4) +4πn, n∈ Z
{(π/12)–(2π/3)+ (4π/3)n < x < (π/12) + (4π/3)m, n ∈ Z

Осталось выбрать пересечение множеств.

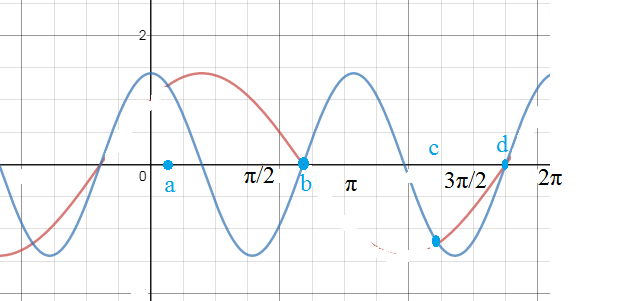
Cм. графиечкое решение неравенства на рис.2

y=sinx+cosx – график красного цвета
y=√2cos2x – график синего цвета

Красный выше синего на отрезках
[a+2πm;b+2πm] m∈ Z
и
на отрезках
[с+2πn;d+2πn] n∈ Z