Задача 37679 ...
Условие
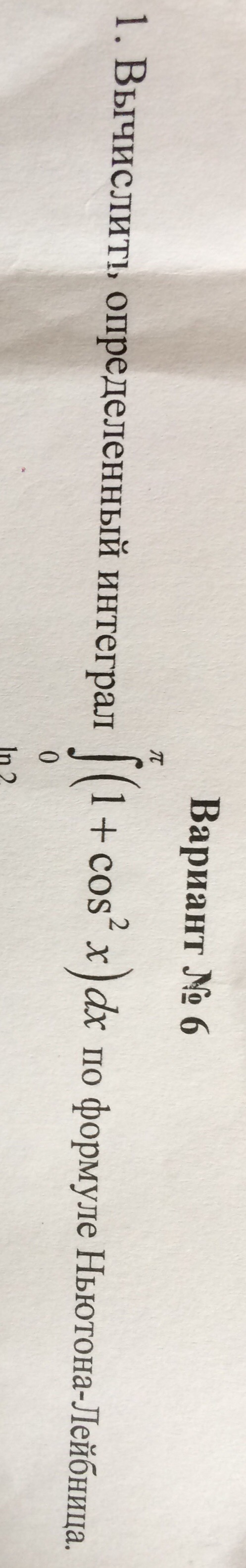
математика ВУЗ
1103
Все решения
∫ ^(π)_(0)(1+cos^2x)dx=(3/2) ∫ ^(π)_(0)dx + (1/2)∫ ^(π)_(0)cos2xdx=
=(3/2)(x)|^( π)_(0) +(1/2)*(1/2)(sin2x)|^(π)_(0)= [b](3/2)π[/b]
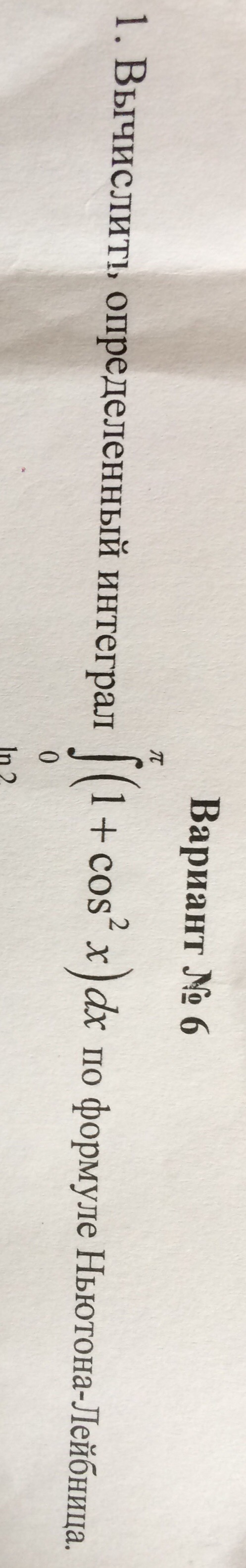
∫ ^(π)_(0)(1+cos^2x)dx=(3/2) ∫ ^(π)_(0)dx + (1/2)∫ ^(π)_(0)cos2xdx=
=(3/2)(x)|^( π)_(0) +(1/2)*(1/2)(sin2x)|^(π)_(0)= [b](3/2)π[/b]