Задача 37622 log(1/3)(x^2-10x+10)=0 log3(7x^2-200) =...
Условие
log3(7x^2-200) = log350x
...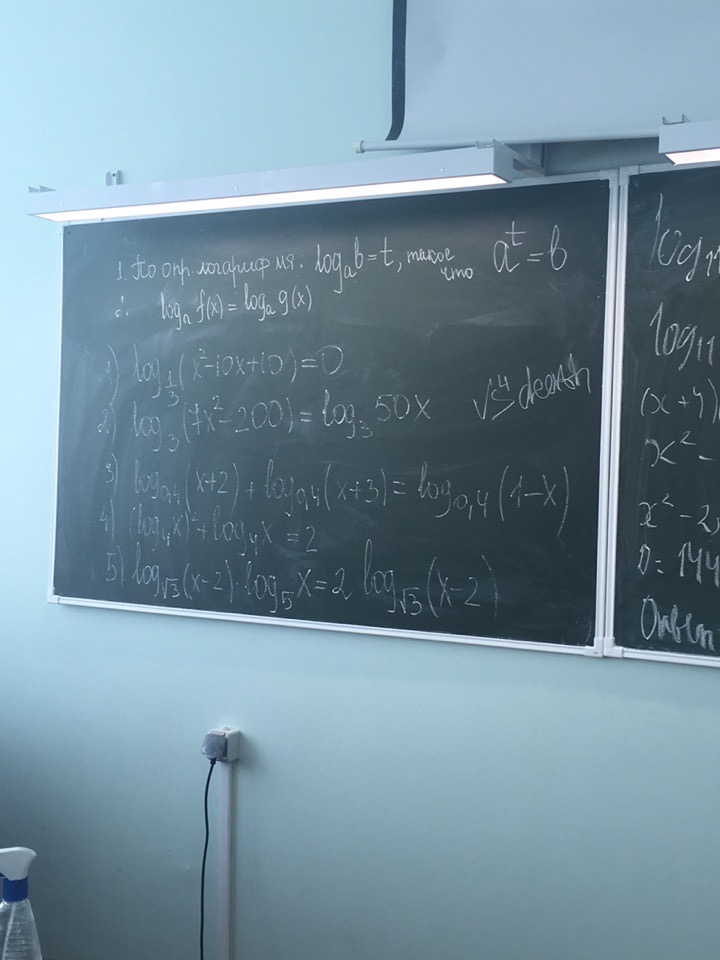
Решение
По определению логарифма
a^(t)=b
x^2-10x+10=(1/3)^(0)
x^2-10x+10=1
x^2-10x+9=0
D=100-36=64
x_(1)=(10-8)/2=1; x_(2)=(10+8)/2=9
О т в е т. 1;9
2.
Логарифмическая функция монотонно возрастает.
Значит каждое свое значение принимает ровно один раз
Если значения функции равны, то и аргументы равны
7x^2-200=50x
7x^2-50x-100=0
D=2500-4*7*(-100)=5300
x_(1)=(50-10sqrt(53))/2; x_(2)=(50+10sqrt(53))/2;
x_(1) < 0 значит log_(3)50x не существует
О т в е т. (50+10sqrt(53))/2;
3.
ОДЗ:
{x+2> 0 ⇒ x > -2
{x+3 > 0 ⇒ x > -3
{1-x > 0 ⇒ x < 1
x ∈ (-2;1)
Заменим сумму логарифмов логарифмом произведения
log_(0,4)(x+2)*(x+3)=log_(0,4)(1-x)
(х+2)*(х+3)=1-х
x^2+5x+6=1-x
x^2+6x+5=0
D=36-20=16
x_(1)=(-6-4)/2=-5; x_(2)=(-6+4)/2=-1
х_(1) не принадлежит ОДЗ
О т в е т. -1
4.
ОДЗ: х > 0
Квадратное уравнение относительно log_(4)x
Замена переменной:
log_(4)x=t
t^2+t=2
t^2+t-2=0
D=9
t_(1)=(-1-3)/2=-2; t_(2)=(-1+3)/2=1
log_(4)x=-2 или log_(4)x=1
x=4^(-2) или x=4
x=1/16
Оба корня удовлетворяют ОДЗ
О т в е т. 1/16; 1
5.
ОДЗ:
{x-2>0 ⇒ x > 2
{x>0
ОДЗ: х ∈ (2;+ ∞ )
log_(sqrt(3))(x-2)*log_(5)x - 2log_(sqrt(3))(x-2)=0
log_(sqrt(3))(x-2) *(log_(5)x -2)=0
log_(sqrt(3))(x-2) =0 или log_(5)x -2=0
x-2=(sqrt(3))^(0) или log_(5)x =2
x-2=1 или x=5^2
х=3 или x=25
Оба корня входят в ОДЗ
О т в е т. 3; 25
