Задача 37595 ...
Условие
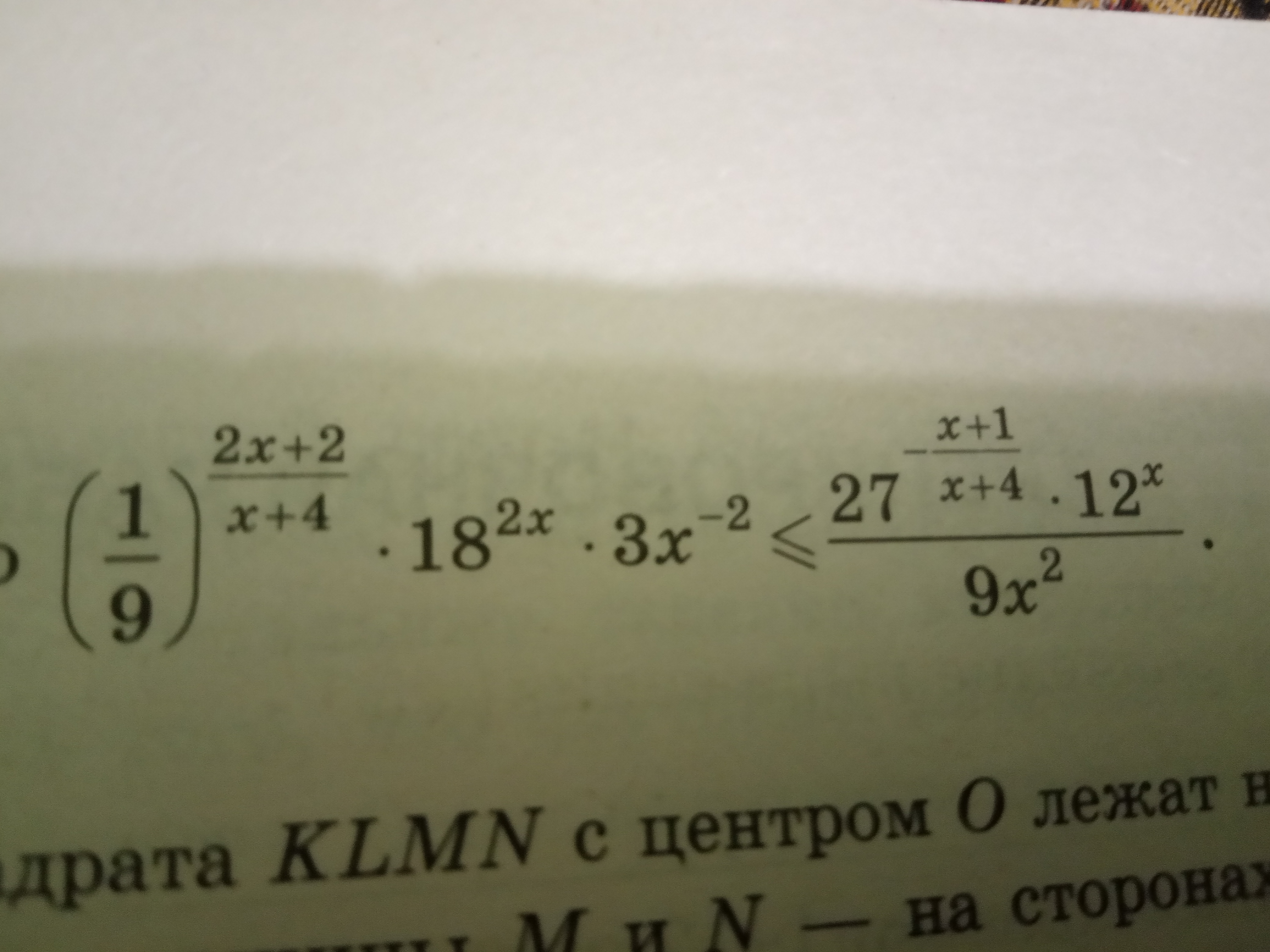
Все решения
{x ≠ 0
{x+4 ≠ 0 ⇒ x ≠ -4
(1/9)^((2x+2)/(x+4))=3^(-4*(x+1)/(x+4))
27^(-(x+1)/(x+4))=3^(-3(x+1)/(x+4))
18^(2x)=(2*3^2)^(2x)=2^(2x)*3^(4x)=4^(x)*3^(4x)
3x^(-2)=3/x^2
12^(x)=(3*4)^(x)=3^(x)*4^(x)
1/(9x^2)=3^(-2)/x^2
Неравенство примет вид:
3^(-4*(x+1)/(x+4)) * 4^(x)*3^(4x)*3/x^2 ≤ =3^(-3(x+1)/(x+4))*3^(x)*4^(x)*3^(-2)/x^2
4^(x) > 0 при любом х
x^2>0 при любом х ≠ 0
Можно сократить на 4^(x)/x^2
3^(-4*(x+1)/(x+4)) * 4^(x)*3^(4x)*3/x^2 ≤ =3^(-3(x+1)/(x+4))*3^(x)*4^(x)*3^(-2)/x^2
3^(-4(x+1)/(x+4) + 4x + 1) ≤ 3^(-3(x+1)/(x+4)+ x - 2)
Показательная функция с основанием 3 возрастает, поэтому
-4(x+1)/(x+4) + 4x + 1 ≤ -3(x+1)/(x+4) + x - 2
-(х+1)/(x+4)+3x+3 ≤0;
(x+1)*(-1+3x+12)/(x+4) ≤ 0
(x+1)*(3x+11)/(x+4) ≤ 0
Решаем методом интервалов
Нули числителя:
х+1=0 или 3х+11=0
х=-1 или х=-11/3
Отмечаем на ОДЗ сплошным кружком ( здесь квадратные скобки)
Нули знаменателя:
x+4=0
x=-4
Отмечаем на ОДЗ пустым кружком ( здесь круглые скобки)
___–___ (–4) __+__ [–11/3] ____–___ [-1] _+__ (0) _+__
О т в е т ( – ∞ ;–4) U [–11/3;-1]
