Задача 37594 Из семян данного растения обычно всходит...

dianatyshenko

2019-05-26 14:41:25

Из семян данного растения обычно всходит 80%. Найти вероятность того, что из 500 семян взойдет 440 и наивероятнейшее число всходов

sova

2019-05-26 15:24:12

★

Повторные испытания с двумя исходами
p=80/100=0,8 - вероятность события в одном испытании
q=1-p=1-0,8=0,2- вероятность того, что событие не наступит в одном испытании

Формула нахождения наивероятнейшего числа:
np - q ≤ k_(o) ≤ np+p

n=500
p=0,8

np=500*0,8=400

400-0,2 ≤ k_(o) ≤ 400+0,2
k_(o)=400 - наивероятнейшее число

Применяем локальную теорему Лапласа
P_(n)(k)≈(1/sqrt(npq))*φ((k-np)/sqrt(npq))

npq=500*0,8*0,2=80
sqrt(npq)=sqrt(80)≈9
(k-np)/sqrt(npq)=(440-400)/9=(40/9)

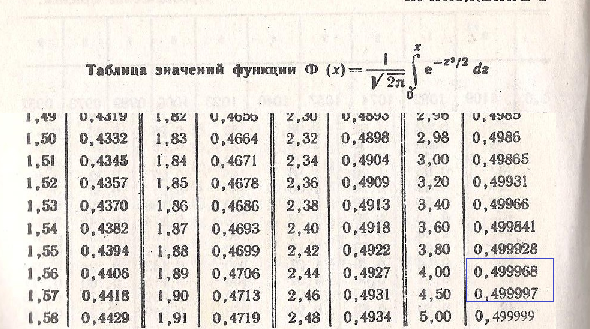
P_(500)(440)≈ (1/9) *φ(40/9)=(1/9)**φ(4,4)( cм приложение)
=(1/9)*0,5=5/90= [b]1/18 [/b]