Задача 37580 Найти объем тела, ограниченного...
Условие
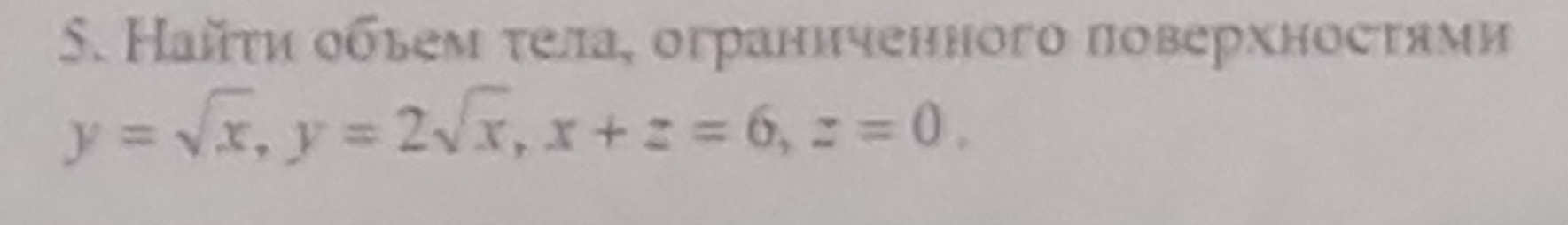
Решение
y= sqrt(x)
y=2sqrt(x)
и линией, которую оставит плоскость z=6-x на пл. хОу.
Находим линию пересечения двух плоскостей
z=0 и z=6-х
6-x=0
x=6
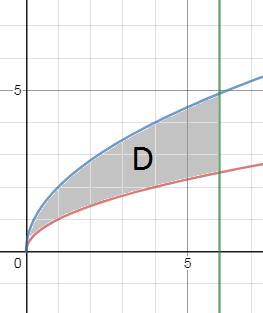
См. область D
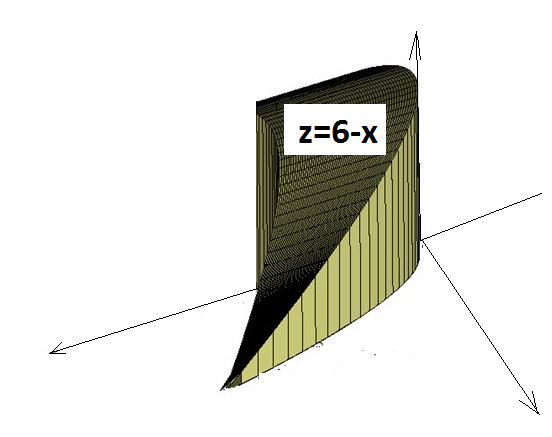
Само тело, представляет из себя криволинейный цилиндр, расположенный над областью D, образующие которого параллельны оси Оz/
z=6-x - плоскость, которая сверху "накрывает тело"
Примерный рис.
V= ∫ ∫ _(D) (6-x)dxdy= ∫^(6)_(0)dx ∫ ^(2sqrt(x)_(sqrt(x) (6-x) dy=
= ∫^(6)_(0)((6-x)*y)|^(2sqrt(x)_(sqrt(x)dx=
= ∫^(6)_(0)(6-x)*(2sqrt(x)-sqrt(x))dx=
= ∫^(6)_(0)(6-x)*sqrt(x)dx=
= ∫^(6)_(0)(6*sqrt(x)-xsqrt(x))dx=