Задача 37568 ...
Условие
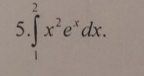
математика ВУЗ
792
Решение
★
dv=e^(x)dx
du=2xdx
v=e^(x)
∫ ^(2)_(1)x^2*e^(x)dx=(x^2*e^(x))|^(2)_(1)- ∫ ^(2)_(1)e^(x)*2xdx=
=(x^2*e^(x))|^(2)_(1)- 2*∫ ^(2)_(1)e^(x)*xdx=
u=x
dv=e^(x)dx
du=dx
v=e^(x)
=(x^2*e^(x))|^(2)_(1)- 2*(x*e^(x))|^(2)_(1)+2∫ ^(2)_(1)e^(x)dx=
=(x^2*e^(x))|^(2)_(1)- 2*(x*e^(x))|^(2)_(1)+2*(e^(x))| ^(2)_(1)=
=4e^2-e-2*2e^2+2e+2e^2-2e= [b]2e^2-e[/b]