Задача 37559 Помогите вычислить несобственный...
Условие
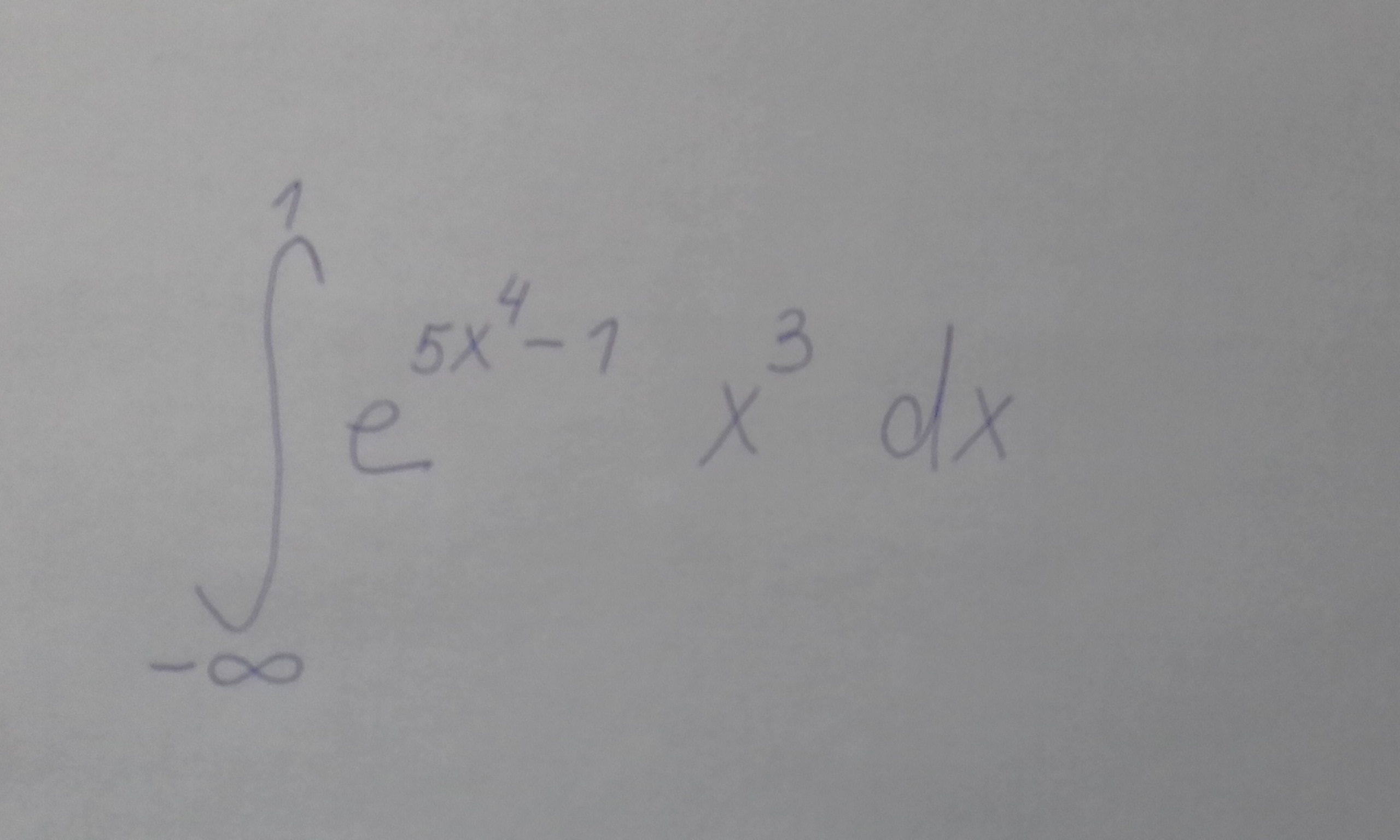
математика ВУЗ
678
Решение
★
d(5x^4-1)=20x^3dx
x^3dx=(1/20)d(5x^4-1)
∫e^(5x^4-1)x^3dx=(1/20) ∫e^(5x^4-1)d(5x^4-1)=(1/20) ∫e^(u)du
=(1/20)e^(u)+C=(1/20)e^(5x^4-1)+C
F(x)=(1/20)e^(5x^4-1)+C
По определению несобственного интеграла первого рода
∫ ^(1)_(- ∞ )e^(5x^4-1)*x^3dx=
=lim_(A→ - ∞ ) F(х)| ^(1)_(A )=
=(1/20)*lim_(A→ - ∞ )e^(5x^4-1)|^(1)_(A)=
=(1/20)*e^(5-1)-(1/20)lim_(A→ - ∞ )e^(5A^4-1)=
=(e^4/20)-(1/20)*e^(+ ∞)= - ∞
Расходится.