Задача 375 На V-T диаграмме изображен цикл 1-2-3-4...
Условие
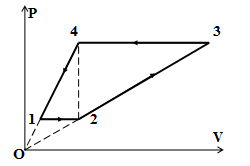
физика 10-11 класс
3970
О решение...
На нашем сайте такое бывает редко, но решение к данной задаче еще никто не написал.
Что Вы можете сделать?
- Выставите данный вопрос вновь. Перейдите на главную страницу.
- Найдите похожую задачу. Используйте поиск.