Задача 37419 Представить двойной интеграл. (рис) где...

foxy

2019-05-21 20:38:27

Представить двойной интеграл. (рис)

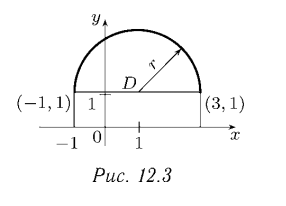
где D — области, указанные на рис. 12.1, 12.2, 12.3, 12.4, в виде суммы двукратных интегралов (с наименьшим числом слагаемых). Фигуры, показанные на рис. 12.3 и 12.4, составлены из прямых линий и дуг окружностей.

sova

2019-05-21 20:58:44

★

Уравнение окружности
(x-1)^2+(y-1)^2=4

(y-1)^2=4-(x-1)^2

y-1=sqrt(4-(x-1)^2)

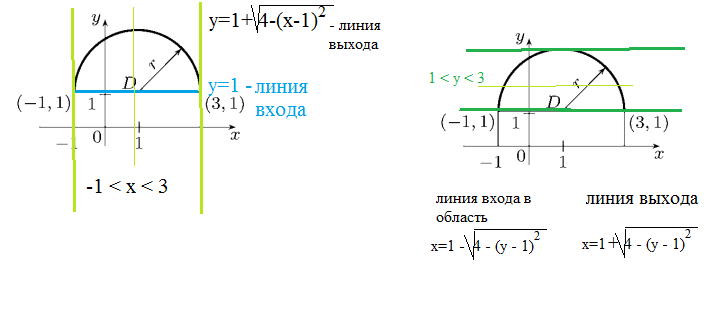
y=1+sqrt(4-(x-1)^2))



D: -1 < x < 3

1 < y < 1+sqrt(4-(x-1)^2)

∫ ∫ _(D)f(x;y)dxdy= ∫^(3) _(-1)dx ∫ ^(1+sqrt(4-(x-1)^2))_(1)f(x;y)dy

или


(x-1)^2+(y-1)^2=4

(х-1)^2=4-(у-1)^2

х-1=sqrt(4-(у-1)^2)

х=1+sqrt(4-(y-1)^2))


D: 1 < y < 3
1-sqrt(4-(y-1)^2) < x < 1+sqrt(4-(y-1)^2)

∫ ∫ _(D)f(x;y)dxdy= ∫^(3) _(1)dy ∫ ^(1+sqrt(4-(y-1)^2))_(1-sqrt(4-(y-1)^2))f(x;y)dx