Задача 37393 ...

tatarelinagood

21 мая 2019 г. в 15:18

1) Решить биквадратное уравнение

2x⁴–x²–1=0

2) Решить систему уравнений

system{y²+2x=2;x+y=1}

3) Решить систему неравенств

system{x²–6x+8 ≤ 0;3x–8 ≥ 0}

sova

21 мая 2019 г. в 15:24

1)
Замена переменной:
x²=t
x⁴=t²

2t²–t–1=0
D=1–4·2·(–1)=9

t₁=(1–3)/4=–1/2; t₂=(1+3)/4=1

Обратный переход

x²=–1/2 – уравнение не имеет корней
x²=1 ⇒ x= ± 1

О т в е т. –1; 1

2.
Из второго уравнения выражаем у и подставляем в первое:
{(1–x)²+2x=1
{y=1–x

1–2х+x²+2x=1
x²=0
x=0
y=1–x=1–0=1

О т в е т. (0;1)

3.
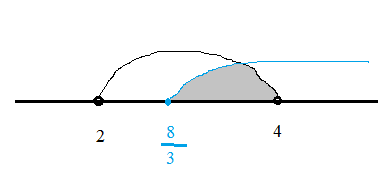
Решаем первое неравенство системы
x²–6x+8 ≤ 0
D=(–6)²–4·8=36–32=4
х₁=(6–2)/2=2; х₂=(6+2)/2=4
2 ≤ х ≤ 4

{2 ≤ х ≤ 4
{x ≥ 8/3

О т в е т. [8/3;4]