Задача 37254 ...
Условие
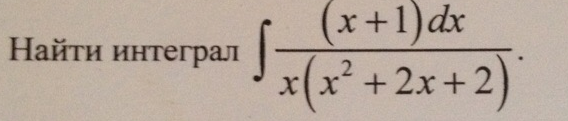
математика ВУЗ
802
Все решения
(x+1)/(x*(x^2+2x+2))= (A/x)+(Mx+N)/(x^2+2x+2)
x+1= A*(x^2+2x+2)+(Mx+N)*x
0=A+M
1=2A+N
1=2A
A=1/2
M=-1/2
N=0
= (1/2)∫ dx/(x+1) - (1/2) ∫ xdx/(x^2+2x+2)=
=(1/2)ln|x+1| - (1/4) ∫( 2x+2-2)dx/(x^2+2x+2)=
=(1/2)ln|x+1| - (1/4)ln|x^2+2x+2| +(1/2) ∫ dx/((x+1)^2+1)=
= [b](1/2)ln|x+1| - (1/4)ln|x^2+2x+2| +(1/2) arctgx + C[/b]