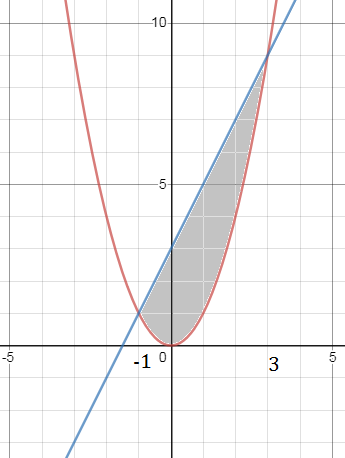
Задача 37230 Найти объем тел, образованных вращением...

vk148511207

2019-05-18 18:25:41

Найти объем тел, образованных вращением вокруг оси ох фигуры, ограниченной линиями: y=x^2, 2x-y+3=0

sova

2019-05-18 21:40:40

★

V_(Ox)=π ∫ ^(3)_(-1)((2x+3)^2-(x^2)^2)dx=

=π ∫ ^(3)_(-1)(4x^2+12x+9-x^4)dx=

=π*((4x^3/3)+(12x^2/2)+9x-(x^5/5))|^(3)_(-1)=

=π*((4/3)*27+6*9+9*3-(243/5)+(4/3)-6+9-(1/5))=...