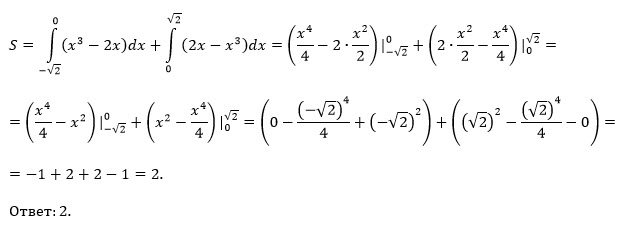Задача 37229 Вычислить площадь фигуры ограниченной...
Условие
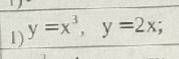
математика ВУЗ
684
Решение
★
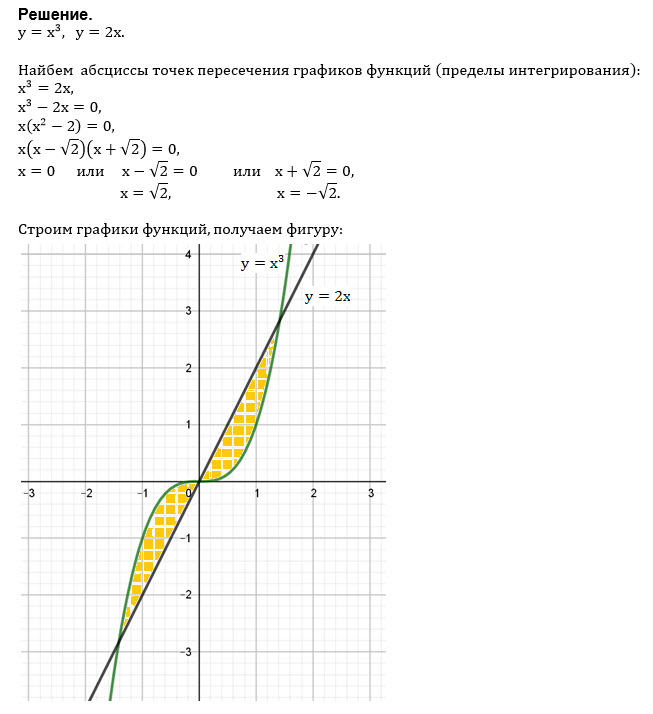
y=x^3 и y=2x
x^3=2x
x*(x^2-2)=0
x=0 или х=± sqrt(2)
S= 2S_(1)=2* ∫ ^(sqrt(2))_(0)(2x-x^3)dx=
=2*(x^2-(x^4/4))|^(sqrt(2))_(0)=2*((sqrt(2))^2-(sqrt(2))^4/4)=
=2*(2-(4/4))=2*(2-1)= [b]2[/b] 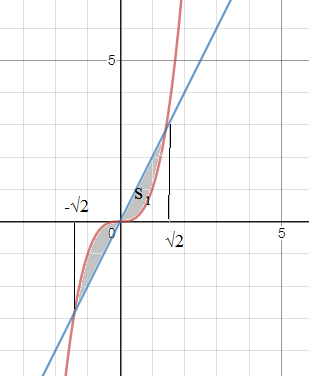
Все решения