Задача 37228 ...
Условие
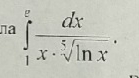
математика ВУЗ
794
Решение
★
=(lnx)^((-1/5)+1)/((-1/5)+1)=(5/4)(lnx)^(4/5)|^(e)_(1)=
=(5/4)*(lne)^(4/5)-(5/4)ln1=(5/4)
Сходится.
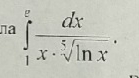
=(lnx)^((-1/5)+1)/((-1/5)+1)=(5/4)(lnx)^(4/5)|^(e)_(1)=
=(5/4)*(lne)^(4/5)-(5/4)ln1=(5/4)
Сходится.