Задача 37227 ...
Условие
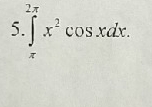
математика ВУЗ
854
Решение
★
du=2xdx
dv=cosxdx
v=sinx
=(x^2*sinx)|^(2π)_(π) - ∫ ^(2π)_(π)sinx*(2x)dx=
=(x^2*sinx)|^(2π)_(π) - 2 ∫ ^(2π)_(π)x*sinxdx=
u=x
du=dx
dv=sinxdx
v=-cosx
=(x^2*sinx)|^(2π)_(π) - 2*(x*(-cosx)|^(2π)_(π)- ∫ ^(2π)_(π)(-cosx)dx)=
=(2π)^2*sin2π-π^2sinπ+2*2πcos2π-2*πcosπ+sinx|^(2π)_(π)=
=4π^2*0-π^2*0+4π-2π*(-1)+sin2π-sinπ=6π