Задача 37226 Решить методом непосредственного...
Условие
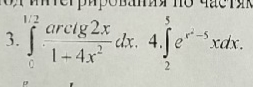
математика ВУЗ
653
Решение
★
d(arctg2x)=2dx/(1+(2x)^2) ⇒ dx/(1+4x^2)=(1/2)d(arctg2x)
=(1/2) ∫^(1/2)_(0) arctg(2x)d(arctg2x)=
=(1/2)*(arctg2x)^2/2=((arctg2x)/4)|^(1/2)_(0)=(1/4)*arctg1-(1/4)*arctg0=
=(1/4)*(π/4)=π/16
4.
d(x^2-5)=2xdx ⇒ xdx=(1/2)d(x^2-5)
=(1/2) ∫ ^(5)_(2) e^(x^2-5)d(x^2-5)=(1/2)e^(x^2-5)|^(5)_(2)=
= [b](1/2)e^(20)-(1/2)e^(-1)[/b]