Задача 37192 8/(10x) = (10/3)^(log(x)(3/8))...
Условие
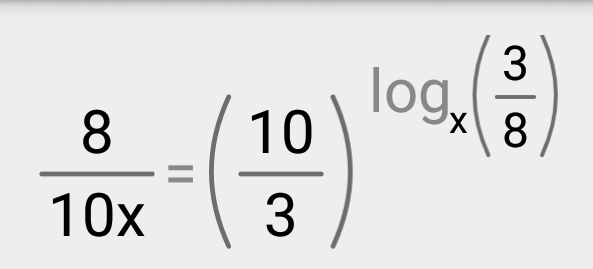
математика 10-11 класс
830
Все решения
x>0;
x ≠ 1
x=3/10 - корень уравнения, так как
При х=3/10
слева получаем
8/(10*(3/10))=8/3
При x=3/10 справа получаем
(10/3)^(log_(3/10)(3/8))= (10/3)^(log_((10/3)^(-1))3/8)=
=(10/3)^(-log_(10/3)(3/8))=(10/3)^(log_(10/3)(3/8)^(-1))=
основное логарифмическое тождество
=(3/8)^(-1)=8/3
8/3=8/3
Функция y=8/(10x), график гипербола
на х>0 монотонно убывает
Функция y=(10/3)^(t) , t=log_(x)(3/8)
- показательная функция с основанием (10/3)>1 монотонно возрастает
Монотонно убывающая и монотонно возрастающая функция пересекаются только в одной точке!
О т в е т. х=3/10