Задача 37165 Решить неравенство (15 номер профиля)...
Условие
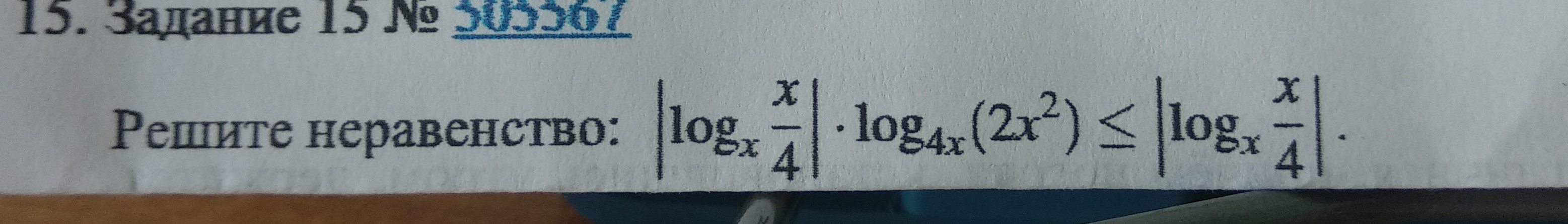
Все решения
{x>0; (x/4) > 4x >0; 2x^2>0 ⇒ [b]x>0[/b]
{x ≠ 1
{4x ≠ 1 ⇒ x ≠ 1/4
х ∈ (0;1/4)U(1/4;1)U(1;+ ∞ )
|log_(x)(x/4)|*(log_(4x)(2x^2)-1) ≤ 0
|log_(x)(x/4)|≥0 при любом х из ОДЗ
При log_(x)(x/4)=0 получаем решение неравенства
x/4=1;
[b]х=4[/b]
[b]log_(4x)(2x^2)- 1 ≤ 0[/b]
log_(4x)(2x^2) ≤ 1
1=log_(a)a при любом a>0; a ≠ 1
log_(4x)(2x^2) ≤ log_(4x)(4x)
Два случая
Первый:
(1)
4х >1, логарифмическая функция возрастает. Большему значению функции соответствует большее значение аргумента
2x^2 ≤ 4x
Cистема
[b]{4x-1>0
{2x^2-4x ≤ 0[/b]
{x>1/4
{0≤x ≤2
о т в е т. (1) (1/4;2]
Второй:
(1)
0 < 4х <1, логарифмическая функция убывает. Большему значению функции соответствует меньшее значение аргумента
2x^2 ≥ 4x
Cистема
[b]{0<4x-1<0
{2x^2-4x ≥0 [/b]
{0<x<1/4
{x ≤ 0 или x ≥ 2
о т в е т. (2) Нет решения
С учетом ОДЗ получаем
О т в е т. [b](1/4;1) U(1;2] U {4}[/b]
____________________________________________________
PS
Так как в обеих системах выражения слева в каждом неравенстве одинаковые, то произведение множителей неотрицательно.
Поэтому вместо решения двух систем можно решить на ОДЗ неравенство:
(4x-1)*(2x^2-4x) ≤ 0
2x*(4x-1)*(x-2) ≤ 0
(0) __+__ (1/4)__-__ (1) ___-__ [2] __+__
(1/4; 1) U (1;2]
Это неравенство можно получить применив [b]метод рационализации к решению log_(4x)(2x^2) ≤ 1[/b]
Тогда решение будет еще проще:
[b]2 cпособ.[/b]
_____________________________________________________
ОДЗ:
{x>0; (x/4) > 4x >0; 2x^2>0 ⇒ [b]x>0[/b]
{x ≠ 1
{4x ≠ 1 ⇒ x ≠ 1/4
х ∈ (0;1/4)U(1/4;1)U(1;+ ∞ )
|log_(x)(x/4)|*(log_(4x)(2x^2)-1) ≤ 0
|log_(x)(x/4)|≥0 при любом х из ОДЗ
При log_(x)(x/4)=0 получаем решение неравенства
x/4=1;
[b]х=4[/b]
[b]log_(4x)(2x^2)- 1 ≤ 0[/b]
Применяем [b]метод рационализации логарифмических неравенств[/b]
log_(4x)(2x^2) ≤ 1
(4x-1)*(2x^2-4x) ≤ 0
2x*(4x-1)*(x-2) ≤ 0
(0) __+__ (1/4)__-__ (1) ___-__ [2] __+__
(1/4; 1) U (1;2]
О т в е т. [b](1/4;1) U(1;2] U {4}[/b]
