Задача 37141 Решить систему двух...
Условие
x+2y=13
2log(4)x - log(4)(2y-1)=0.5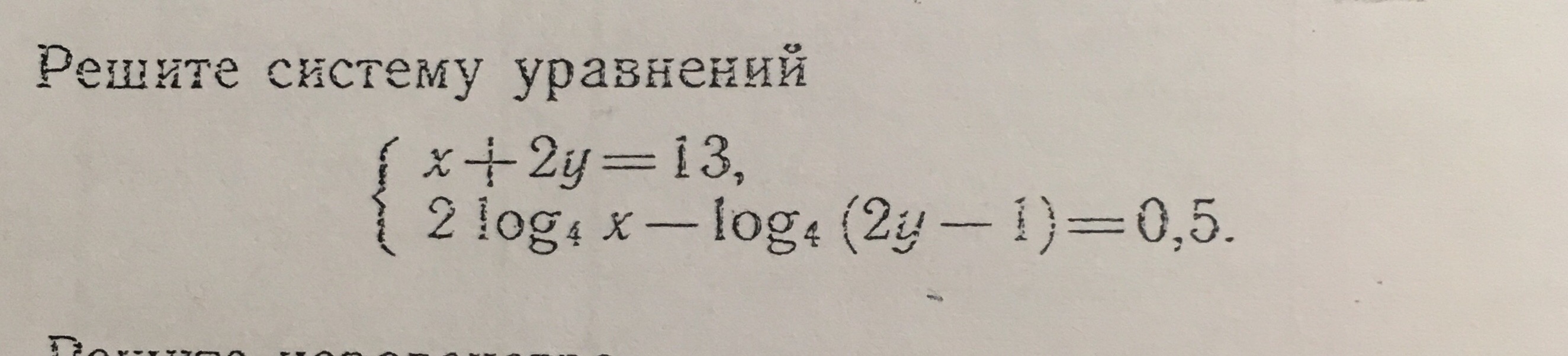
математика 10-11 класс
1846
Решение
★
2log_(4)x=log_(4)x^2
Тогда
log_(4)x^2-log_(4)(2y-1)=0,5*1
Так как 1=log_(4)4
log_(4)x^2-log_(4)(2y-1)=0,5*log_(4)4
log_(4)x^2-log_(4)(2y-1)=log_(4)4^(0,5)
log_(4)x^2=log_(4)(2y-1)+log_(4)2
log_(4)x^2=log_(4)2*(2y-1)
x^2=2*(2y-1)
Система принимает вид:
{x+2y=13 ⇒ x= 13-2y
{x^2=2*(2y-1)
(13-2y)^2=2*(2y-1)
169-52y+4y^2=4y-2
4y^2-56y+171=0
D=56^2-4*4*171=3136-2736=400
y_(1)=(56-20)/8=26/8=13/4; y_(2)=(56+20)/8=76/8=38/4
x_(1)=13/2 x_(2)=-6 не удовлетворяет условию log_(4)(-6) не сущ.
О т в е т. [b](13/2; 13/4)[/b]