Задача 37140 решите уравнение 2^(-|x|)=1/(2sqrt(2))...
Условие
2^(-|x|)=1/(2sqrt(2)) *(|x+1|+|x-1|)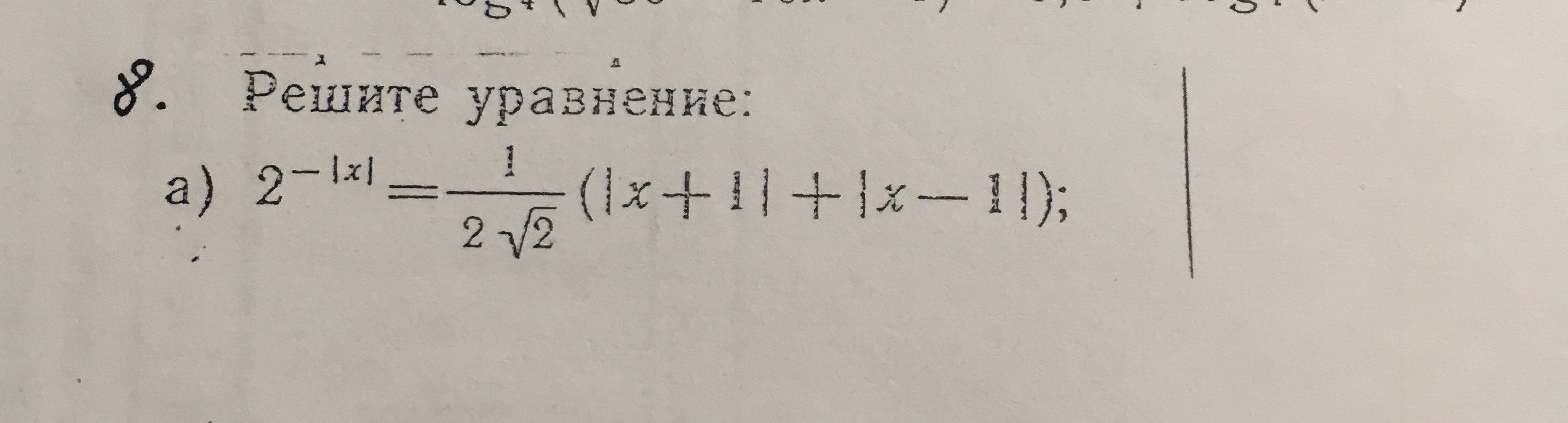
Решение
х=-1; х=0; х=1
Эти точки разбивают числовую прямую на 4 интервала.
Раскрываем модуль на каждом из четырех интервалов:
(1)
[b](- ∞ :-1][/b]
|x|=-x
|x+1|=-x-1
|x-1|=-x+1
Уравнение принимает вид:
[b]2^(x)=(1/2sqrt(2))*(-x-1-x+1)[/b]
2sqrt(2)*2^(x)=-2x
2^(x+(1/2))=-x
Решаем графически.
(см. рис.1)
единственная точка пересечения, одна кривая возрастает, вторая - прямая убывает.
х= - 0,808 ∉ (- ∞ :-1]
Уравнение не имеет корней на этом интервале
(2)
[b](-1;0][/b]
|x|=-x
|x+1|=x+1
|x-1|=-x+1
Уравнение принимает вид:
[b]2^(x)=(1/2sqrt(2))*(x+1-x+1)[/b]
2sqrt(2)*2^(x)=1
2^(x+(1/2))=1
Решаем графически.
(см. рис.2)
единственная точка пересечения, одна кривая возрастает, вторая -
константа
[b]x=-0,5 - корень, принадлежит интервалу (-1;0][/b]
(3)
[b](0;1][/b]
|x|=x
|x+1|=x+1
|x-1|=-x+1
Уравнение принимает вид:
[b]2^(-x)=(1/2sqrt(2))*(x+1-x+1)[/b]
sqrt(2)*2^(-x)=1
Решаем графически.
(см. рис.3)
единственная точка пересечения, одна кривая убывает, вторая -
константа
[b]x=0,5 - корень, принадлежит интервалу (0;1][/b]
(4)
[b](1;+ ∞ )[/b]
|x|=x
|x+1|=x+1
|x-1|=x+1
Уравнение принимает вид:
[b]2^(-x)=(1/2sqrt(2))*(x+1+x-1)[/b]
sqrt(2)*2^(-x)=х
Решаем графически.
(см. рис.4)
единственная точка пересечения, одна кривая убывает, вторая - прямая( возрастает)
x=0,808 не принадлежит интервалу(1;+ ∞ )
Уравнение не имеет корней на этом интервале
О т в е т. [b] ± 0,5 [/b]