Задача 37139 sqrt(4cos(2x)-2sin(2x)) = 2cos(x)...
Условие
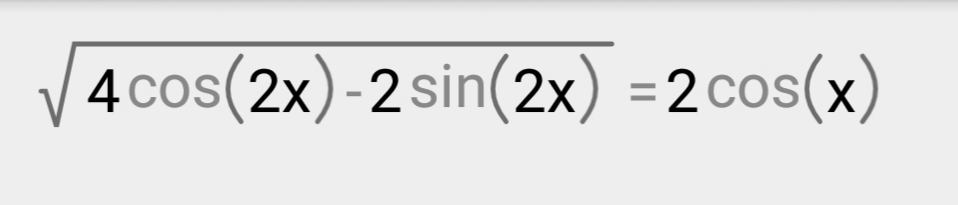
Решение
Возводим в квадрат
4 cos2x-2sin2x=4cos^2x
2сos^2x=1+cos2x
тогда уравнение принимает вид:
4 cos2x-2sin2x=2*(1+cos2x)
2cos2x-2sin2x=2
cos2x-sin2x=1
cos2x=sin((π/2)-2x)
sin((π/2)-2x)- sin2x=1
Формула sin α - sin β=
2sin((π/4)-2x)*cos(π/4)=1
sin((π/4)-2x)=1/sqrt(2)
sin(2x-(π/4))=-1/sqrt(2)
2x-(π/4)=(-1)^(k)*(-π/4) +πk, k ∈ Z
2x=(π/4)+(-1)^(k)*(-π/4) +πk, k ∈ Z
x= [b](π/8)+(-1)^(k)*(-π/8) +(π/2)*k, k ∈ Z[/b]- о т в е т.
Но лучше решение уравнения sin(2x-(π/4))=-1/sqrt(2)
записать в виде серии двух ответов:
2x-(π/4)= [b](-π/4) +2πn, n ∈ Z[/b] или 2х-(π/4)= [b](-3π/4) +2πm, m ∈ Z
[/b]
2x=2πn, n ∈ Z или 2х-(π/4)=(-3π/4) +2πm, m ∈ Z
x=πn, n ∈ Z или 2x=(-π/2)+2πm, m ∈ Z ⇒ x=(-π/4)+πm, m ∈ Z
С учетом ОДЗ: cosx≥ 0
О т в е т. 2*πn, n ∈ Z ; (-π/4)+2πm, m ∈ Z