Задача 37132 ...

nashipitsina

2019-05-16 17:55:53

Вычислите интеграл
∫ ∫ (x^2 +y^2)dxdy,
D
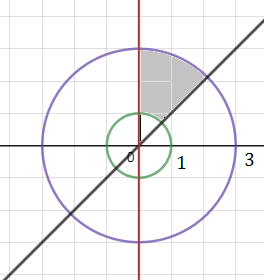
где область D ограничена кривыми x^2+y^2=1, x^2+y^2=9, x=0, y=x, x>0.

sova

2019-05-16 18:06:29

Переход к полярным координатам
x= ρ cos φ
y= ρ sin φ

1 < ρ <3

π/4 < φ < π/2 cм. рис.

∫ ∫ _(D)(x^2+y^2)dxdy= ∫ ^(3)_(1)( ∫^( π/2)_(π/4) ρ ^2* ρ d φ) d ρ =

= ∫ ^(3)_(1) ρ ^3*( φ)|^( π/2)_(π/4) dρ =

= (π/4)* ( ρ ^(4)/4)|^(3)_(1)=(π/16)*(3^4-1^4)=

=(π/16)*(81-1)=80*(π/16)= [b]5π[/b]

РS.

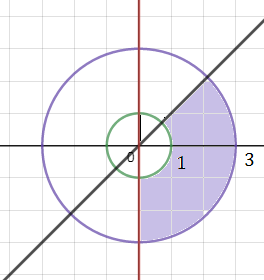
Выбрала меньшую область, но в принципе и на рис. 2 область тоже удовлетворяет условию.

В этой области угол меняется от (-π/2) до (π/4)

Тогда (π/4)-(-π/2)=3π/4

и тогда ответ (3π/16)*80=15π