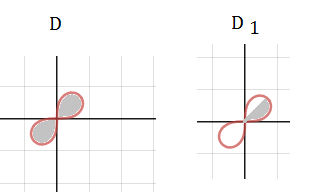
Задача 37130 Вычислить площадь фигуры, ограниченной...
Условие
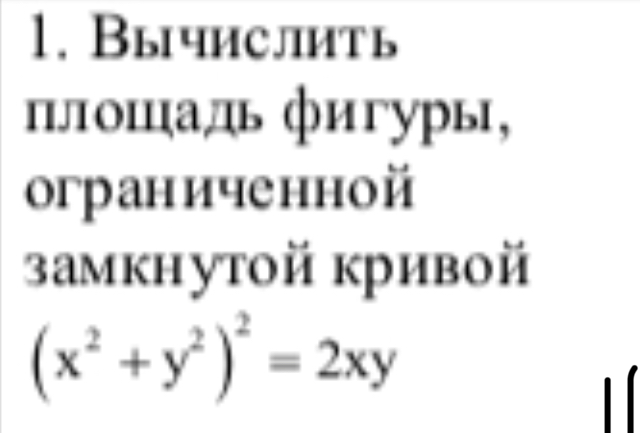
математика ВУЗ
3901
Все решения
x= ρ cos φ
y= ρ sin φ
x^2+y^2=ρ ^2
Уравнение кривой принимает вид:
(ρ ^2)^2=2*ρ cos φ * ρ sin φ
или
ρ ^2=2 cos φ *sin φ
ρ ^2=sin2φ
S= ∫ ∫ _(D)dxdy=4∫ ∫_(D_(1))dxdy=
D_(1):
0 < ρ < sqrt(sin2φ)
0 < φ <( π/4)
=4* ∫ ^(π/4)_(0)( ∫ ^(sqrt(sin2 φ )_(0))ρd ρ )d φ =
считаем внутренний интеграл
=4* ∫ ^(π/4)_(0)( ρ^(2)/2))|^(sqrt(sin2 φ )_(0))d φ =
=2* ∫ ^(π/4)_(0)sin2 φ d φ =
=2*(1/2)(-cos2 φ)|^( π/4)_(0)=
=(-cos(π/2)+cos0)= [b]1[/b]